EntrataSistemi di equazioni lineari. Metodo di Cramer per la risoluzione di sistemi di equazioni lineari
- Sistemi M equazioni lineari con N sconosciuto.
Risoluzione di un sistema di equazioni lineari- questo è un tale insieme di numeri ( x1, x2,..., xn), quando sostituito in ciascuna delle equazioni del sistema, si ottiene l'uguaglianza corretta.
Dove a ij , i = 1, …, m; j = 1,..., n— coefficienti del sistema;
b io , io = 1, …, m- membri gratuiti;
x j , j = 1, …, n- sconosciuto.
Il sistema sopra descritto può essere scritto in forma matriciale: AX = B,
Dove ( UN|B) è la matrice principale del sistema;
UN— matrice del sistema esteso;
X— colonna delle incognite;
B— colonna dei membri liberi.
Se matrice B non è una matrice nulla ∅, allora questo sistema le equazioni lineari sono dette disomogenee.
Se matrice B= ∅, allora questo sistema di equazioni lineari si dice omogeneo. Un sistema omogeneo ha sempre una soluzione zero (banale): x1 = x2 = …, xn = 0.
Sistema congiunto di equazioni lineariè un sistema di equazioni lineari che ha una soluzione.
Sistema incoerente di equazioni lineariè un sistema irrisolvibile di equazioni lineari.
Un certo sistema di equazioni lineari- sta avendo l'unica soluzione sistema di equazioni lineari.
Sistema indefinito di equazioni lineariè un sistema di equazioni lineari con un numero infinito di soluzioni. - Sistemi di n equazioni lineari con n incognite
Se il numero di incognite è uguale al numero di equazioni, la matrice è quadrata. Il determinante di una matrice è detto determinante principale di un sistema di equazioni lineari ed è indicato con il simbolo Δ.
Metodo Cramer per risolvere i sistemi N equazioni lineari con N sconosciuto.
Regola di Cramer.
Se il determinante principale di un sistema di equazioni lineari non è uguale a zero, allora il sistema è coerente e definito e l'unica soluzione si calcola utilizzando le formule di Cramer:
dove Δ i sono determinanti ottenuti dal determinante principale del sistema Δ mediante sostituzione io la quarta colonna alla colonna dei membri gratuiti. . - Sistemi di m equazioni lineari con n incognite
Teorema di Kronecker-Capelli.
Affinché un dato sistema di equazioni lineari sia coerente, è necessario e sufficiente che il rango della matrice del sistema sia uguale al rango della matrice estesa del sistema, suonato(Α) = suonato(Α|B).
Se raggio(Α) ≠ raggio(Α|B), allora il sistema ovviamente non ha soluzioni.
Se suonato(Α) = suonato(Α|B), allora sono possibili due casi:
1) rango(Α) = n(numero di incognite) - la soluzione è unica e può essere ottenuta utilizzando le formule di Cramer;
2) rango(Α)< n - ci sono infinite soluzioni. - Metodo di Gauss per la risoluzione di sistemi di equazioni lineari
Creiamo una matrice estesa ( UN|B) di un dato sistema dai coefficienti delle incognite e dai membri di destra.
Il metodo gaussiano o metodo di eliminazione delle incognite consiste nel ridurre la matrice estesa ( UN|B) utilizzando trasformazioni elementari sulle sue righe in una forma diagonale (nella forma triangolare superiore). Ritornando al sistema di equazioni, vengono determinate tutte le incognite.
Le trasformazioni elementari sulle stringhe includono quanto segue:
1) scambiare due linee;
2) moltiplicare una stringa per un numero diverso da 0;
3) aggiungere un'altra stringa a una stringa, moltiplicata per un numero arbitrario;
4) lanciando una linea zero.
Corrisponde la matrice estesa ridotta in forma diagonale sistema lineare, equivalente a questo, la cui soluzione non presenta difficoltà. . - Sistema di equazioni lineari omogenee.
Un sistema omogeneo ha la forma:
corrisponde all'equazione della matrice AX = 0.
1) Un sistema omogeneo è sempre coerente, poiché r(A) = r(A|B), esiste sempre una soluzione zero (0, 0, …, 0).
2) Affinché un sistema omogeneo abbia soluzione diversa da zero è necessario e sufficiente che r = r(A)< n , che equivale a Δ = 0.
3) Se R< n , allora ovviamente Δ = 0, allora sorgono incognite libere c 1 , c 2 , …, c n-r, il sistema ha soluzioni non banali e ce ne sono infinite.
4) Soluzione generale X A R< n può essere scritto in forma matriciale come segue:
X = c 1 X 1 + c 2 X 2 + … + c n-r X n-r,
dove sono le soluzioni X 1 , X 2 , …, X n-r costituiscono un sistema fondamentale di soluzioni.
5) Sistema fondamentale le soluzioni possono essere ottenute dalla soluzione generale di un sistema omogeneo:
,
se impostiamo in sequenza i valori dei parametri uguali a (1, 0, …, 0), (0, 1, …, 0), …, (0, 0, …, 1).
Espansione della soluzione generale in termini del sistema fondamentale delle soluzioniè la registrazione di una soluzione generale sotto forma di combinazione lineare di soluzioni appartenenti al sistema fondamentale.
Teorema. Affinché un sistema di equazioni lineari omogenee abbia soluzione diversa da zero è necessario e sufficiente che Δ ≠ 0.
Quindi, se il determinante Δ ≠ 0, allora il sistema ha un'unica soluzione.
Se Δ ≠ 0, allora il sistema di equazioni lineari omogenee ha un numero infinito di soluzioni.
Teorema. Affinché un sistema omogeneo abbia una soluzione diversa da zero è necessario e sufficiente che r(A)< n .
Prova:
1) R non può esserci di più N(il rango della matrice non supera il numero di colonne o righe);
2) R< n , Perché Se r = n, allora il determinante principale del sistema Δ ≠ 0, e, secondo le formule di Cramer, esiste un’unica soluzione banale x1 = x2 = … = xn = 0, il che contraddice la condizione. Significa, r(A)< n .
Conseguenza. Per avere un sistema omogeneo N equazioni lineari con N incognite hanno soluzione diversa da zero, è necessario e sufficiente che Δ = 0.
FILIALE DI KOSTROMA DELL'UNIVERSITÀ MILITARE DI PROTEZIONE RCHB
Dipartimento di automazione del controllo delle truppe
Solo per insegnanti
"Approvo"
Capo del dipartimento n. 9
Il colonnello YAKOVLEV A.B.
"____"_______________ 2004
Professore Associato A.I. SMIRNOVA
"QUALIFICAZIONI.
SOLUZIONE DI SISTEMI DI EQUAZIONI LINEARI"
LEZIONE N. 2 / 1
Discusso nella riunione di dipartimento n. 9
"____"_____________ 2004
Protocollo n._____________
Kostroma, 2004.
Introduzione
Determinanti del secondo e terzo ordine.
Proprietà dei determinanti.
Teorema di decomposizione.
Il teorema di Cramer.
Conclusione
Letteratura V.E. Schneider et al.
Corso breve
Matematica superiore, volume I, cap.
2, comma 1.
V.S. Shchipachev, Matematica superiore, capitolo 10, paragrafo 2. INTRODUZIONE
La lezione discute i determinanti del secondo e del terzo ordine e le loro proprietà. E anche il teorema di Cramer, che consente di risolvere sistemi di equazioni lineari utilizzando i determinanti. I determinanti vengono utilizzati anche più avanti nell'argomento “Algebra vettoriale” quando si calcola il prodotto vettoriale di vettori.
1a domanda di studio
DETERMINANTI DEL SECONDO E DEL TERZO
ORDINE Considera una tabella di quattro numeri del modulo I numeri nella tabella sono indicati da una lettera con due indici. Il primo indice indica il numero di riga, il secondo il numero di colonna.
(1)
DEFINIZIONE 1.
Diagonale formata dagli elementi a11; a22 è detta principale, e la diagonale formata dagli elementi di a12; a21 - lato.
Pertanto, il determinante del secondo ordine è uguale alla differenza tra i prodotti degli elementi delle diagonali principale e secondaria.
Tieni presente che la risposta è un numero.
ESEMPI.
Calcolare:
Consideriamo ora una tabella di nove numeri, scritti su tre righe e tre colonne:DEFINIZIONE 2. Determinante del terzo ordine
chiamata espressione della forma:
Elementi a11; a22; a33 – forma la diagonale principale.
Numeri a13; a22; a31 – formare una diagonale laterale.
" + " " – "
Descriviamo schematicamente come si formano i termini più e meno:
Il più comprende: il prodotto degli elementi sulla diagonale principale, i restanti due termini sono il prodotto degli elementi situati ai vertici dei triangoli con basi parallele alla diagonale principale.
I termini meno si formano secondo lo stesso schema rispetto alla diagonale secondaria.
Questa regola per il calcolo del determinante del terzo ordine si chiama
Regola T reugolnikov.
ESEMPI.
Calcola utilizzando la regola del triangolo: COMMENTO. I determinanti sono anche chiamati determinanti.
2a domanda di studio
PROPRIETÀ DEI DETERMINANTI.
.
TEOREMA DI ESPANSIONE
Proprietà 1. Il valore del determinante non cambia se le sue righe vengono scambiate con le colonne corrispondenti.
Rivelando entrambe le determinanti, siamo convinti della validità dell'uguaglianza.
.
La proprietà 1 stabilisce l'uguaglianza delle righe e delle colonne del determinante. Pertanto, formuleremo tutte le ulteriori proprietà del determinante sia per le righe che per le colonne.
.
Proprietà 2. Quando due righe (o colonne) vengono riorganizzate, il determinante cambia segno in quello opposto, mantenendo il suo valore assoluto.
Proprietà 3. Il fattore comune degli elementi di una riga (o colonna) può essere portato oltre il segno del determinante.
Proprietà 4. Se un determinante ha due righe (o colonne) identiche, allora è uguale a zero.
Questa proprietà può essere dimostrata mediante verifica diretta oppure è possibile utilizzare la proprietà 2.
Indichiamo il determinante con D. Quando due identiche prima e seconda riga vengono riorganizzate, non cambierà, ma secondo la seconda proprietà deve cambiare segno, cioè
D = - D Yu 2 D = 0 Yu D = 0.
Proprietà 5. Se tutti gli elementi di una riga (o colonna) sono uguali a zero, allora il determinante è uguale a zero.
.
Questa proprietà può essere considerata come un caso speciale della proprietà 3 quando
Proprietà 7. Il valore del determinante non cambierà se agli elementi di qualsiasi riga (o colonna) vengono aggiunti gli elementi corrispondenti di un'altra riga (o colonna), moltiplicati per lo stesso numero.
.
Dimostrato tramite verifica diretta.
L'utilizzo di queste proprietà può in alcuni casi facilitare il processo di calcolo dei determinanti, soprattutto del terzo ordine.
Per quanto segue avremo bisogno dei concetti di complemento minore e algebrico. Consideriamo questi concetti per definire il terzo ordine.
DEFINIZIONE 3.Minore di un dato elemento di un determinante del terzo ordine è chiamato determinante del secondo ordine ottenuto da un dato elemento cancellando la riga e la colonna all'intersezione delle quali si trova l'elemento dato.
L'elemento minore ai j è indicato con Mi j. Quindi per l'elemento a11 minore
Si ottiene cancellando la prima riga e la prima colonna nel determinante del terzo ordine.
DEFINIZIONE 4.Complemento algebrico dell'elemento del determinante lo chiamano minore moltiplicato per (-1)k, dove k è la somma dei numeri di riga e colonna all'intersezione dei quali si trova questo elemento.
Il complemento algebrico dell'elemento ai j si denota con Ai j.
Pertanto, Ài j = .
Scriviamo le addizioni algebriche per gli elementi a11 e a12.
.
È utile ricordare la regola: il complemento algebrico di un elemento di un determinante è uguale al suo minore con un segno più se la somma dei numeri della riga e della colonna in cui si trova l'elemento è pari, e con un segno meno firmare se la somma è dispari.
ESEMPIO. Trova minori e complementi algebrici per gli elementi della prima riga del determinante:
È chiaro che i minori ed i complementi algebrici possono differire solo nel segno.
Consideriamo senza dimostrazione un teorema importante: il teorema di scomposizione del determinante.
TEOREMA DI ESPANSIONE
Determinante pari alla somma prodotti degli elementi di qualsiasi riga o colonna mediante i loro complementi algebrici.
Usando questo teorema, scriviamo lo sviluppo del determinante del terzo ordine lungo la prima riga.
.
In forma estesa: 
.
L'ultima formula può essere utilizzata come principale quando si calcola il determinante del terzo ordine.
Il teorema di espansione permette di ridurre il calcolo del determinante del terzo ordine al calcolo di tre determinanti del secondo ordine.
Il teorema di scomposizione fornisce un secondo modo per calcolare i determinanti del terzo ordine.
ESEMPI.
Calcolare il determinante utilizzando il teorema di espansione.
utilizzate espansioni lungo la seconda riga.
Pertanto, il determinante del quarto ordine può essere ridotto al calcolo di quattro determinanti del terzo ordine.
3a domanda di studio TEOREMA DI CRAMER
Applichiamo la teoria dei determinanti considerata alla risoluzione di sistemi di equazioni lineari.
Un sistema di due equazioni lineari in due incognite.
(3)
Qui x1, x2 sono incognite;
a11, ..., a22 – coefficienti per le incognite, numerati con due indici, dove il primo indice indica il numero dell'equazione e il secondo indice indica il numero dell'incognita.
b1, b2 sono termini liberi.
Ricordiamo che la soluzione del sistema (3) è intesa come una coppia di valori x1, x2 che, sostituiti in entrambe le equazioni, le trasformano in vere uguaglianze.
Nel caso in cui un sistema abbia un'unica soluzione, questa soluzione può essere trovata utilizzando determinanti del secondo ordine.
DEFINIZIONE 5. Viene chiamato un determinante formato da coefficienti per incognite determinante del sistema.
Indichiamo il determinante del sistema con D.
Le colonne del determinante D contengono rispettivamente i coefficienti di x1 e di x2.
Introduciamo due determinanti aggiuntivi, che si ottengono dal determinante del sistema sostituendo una delle colonne con una colonna di termini liberi:
Consideriamo senza dimostrazione il seguente teorema:
TEOREMA DI CRAMER(per il caso n = 2)
Se il determinante D del sistema (3) è diverso da zero (D n. 0), allora il sistema ha un'unica soluzione, che si trova secondo le formule:
(4)
Le formule (4) sono chiamate formule di Cramer.
ESEMPIO. Risolvi il sistema utilizzando la regola di Cramer.
Risposta: x1 = 3; x2 = -1
2. Sistema di tre equazioni lineari in tre incognite:
(5)
Nel caso di soluzione unica, il sistema (5) può essere risolto utilizzando determinanti del terzo ordine.
Il determinante del sistema D ha la forma:
Introduciamo tre ulteriori determinanti:
Il teorema è formulato in modo simile.
TEOREMA DI CRAMER (per il caso n = 3)
Se il determinante D del sistema (5) è diverso da zero, allora il sistema ha un'unica soluzione, che si trova secondo le formule:
Le formule (6) sono formule di Cramer.
COMMENTO. G. Cramer (1704 – 1752) – matematico svizzero.
Si noti che il teorema di Cramer è applicabile quando il numero di equazioni è uguale al numero di incognite e quando il determinante del sistema D è diverso da zero.
Se il determinante di un sistema è uguale a zero, allora in questo caso il sistema può non avere soluzioni oppure avere un numero infinito di soluzioni. Questi casi sono studiati separatamente e possono essere trovati in dettaglio nella letteratura raccomandata.
Notiamo un solo caso:
Se il determinante del sistema è uguale a zero (D = 0), e almeno uno dei determinanti aggiuntivi è diverso da zero, allora il sistema non ha soluzioni (cioè è incoerente).
Il teorema di Cramer può essere generalizzato a un sistema di n equazioni lineari con n incognite.
Se 
, allora l'unica soluzione al sistema si trova secondo
Formule di Cramer:
Qualificatore aggiuntivo 
si ottiene dal determinante D se contiene una colonna di coefficienti per l'incognita
xi è sostituito da una colonna di membri liberi.
Si noti che i determinanti D, D1, …, Dn sono di ordine n.
CONCLUSIONE
La conferenza ha esaminato un nuovo concetto: un determinante, e ha discusso in dettaglio i determinanti di secondo e terzo ordine, che si incontrano spesso nella pratica. Per il determinante del terzo ordine vengono forniti due metodi di calcolo. Viene considerato il teorema di Cramer, che fornisce un modo pratico per risolvere sistemi di equazioni lineari nel caso in cui la soluzione sia unica. Puoi saperne di più su questo argomento nella letteratura consigliata.
Abstract simili:
Regole per il prodotto di una matrice e un vettore, trovando l'inverso di una matrice e il suo determinante. Trasformazioni elementari di matrici: moltiplicazione per un numero, addizione, riordinamento e cancellazione di righe, trasposizione. Risoluzione di un sistema di equazioni utilizzando il metodo di Gauss.
Questo abstract esamina i determinanti del secondo e del terzo ordine e fornisce esempi di risoluzione di sistemi di equazioni utilizzando il metodo dei determinanti.
Determinazione del complemento algebrico dell'elemento determinante, matrice, sua dimensione e tipologie. Sistema disomogeneo di equazioni algebriche lineari. Risoluzione di un sistema di equazioni utilizzando il metodo di Cramer. Grandezze scalari e vettoriali, loro esempi, scomposizione vettoriale.
Lezione 1.1.Matrici numeriche e operazioni su di esse.
Riepilogo:Il posto dell'algebra lineare e della geometria analitica nelle scienze naturali. Il ruolo degli scienziati domestici nello sviluppo di queste scienze. Il concetto di matrice. Operazioni sulle matrici e loro proprietà.
Una tabella di numeri della forma è chiamata rettangolare matrice dimensioni. Le matrici sono indicate con lettere maiuscole in lettere latine A, B, C, ...Vengono chiamati i numeri che compongono la tabella elementi matrici. Ogni elemento ha due indici e , che indicano rispettivamente il numero di riga () e il numero di colonna () in cui si trova l'elemento. Usato seguenti designazioni matrici
Le due matrici vengono chiamate pari , se hanno la stessa dimensione (es. stesso numero righe e colonne) e se i numeri nei posti corrispondenti di queste matrici sono uguali.
Se il numero di righe di una matrice è uguale al numero delle sue colonne, viene chiamata la matrice piazza
. In una matrice quadrata, il numero di righe (o colonne) è chiamato ordine della matrice. In particolare, una matrice quadrata del primo ordine è semplicemente un numero reale. Di conseguenza lo dicono linea vettoriale
è una matrice di dimensione , e vettore colonna
ha dimensione.
Vengono chiamati gli elementi che giacciono sulla diagonale principale di una matrice quadrata (che va dall'angolo in alto a sinistra all'angolo in basso a destra). diagonale .
Viene detta una matrice quadrata i cui elementi non sulla diagonale principale sono tutti 0 diagonale .
Viene detta una matrice diagonale i cui elementi diagonali sono tutti 1 e tutti gli elementi fuori diagonale sono 0 separare ed è indicato con o , dove n è il suo ordine.
Le operazioni di base sulle matrici sono l'addizione di matrici e la moltiplicazione di una matrice per un numero.
Il lavoro matrici UN il numero è una matrice della stessa dimensione della matrice UN, ciascun elemento del quale viene moltiplicato per questo numero.
Per esempio: 
; 
.
Proprietà dell'operazione di moltiplicazione di una matrice per un numero:
1.l(m UN )=(lm) UN (associatività)
2.l( UN +IN )=l UN +l IN (distributività rispetto all'addizione di matrice)
3. (l+m) UN =)=l UN +m UN (distributività relativa all'addizione di numeri)
Combinazione lineare di matrici UN E IN della stessa dimensione è detta espressione della forma: a UN +b IN , dove a,b sono numeri arbitrari
Matrice somma E IN (questa azione è applicabile solo a matrici della stessa dimensione) è detta matrice CON della stessa dimensione, i cui elementi sono uguali alle somme dei corrispondenti elementi della matrice UN E IN .
Proprietà dell'addizione di matrici:
1)UN +IN =IN +UN (commutatività)
2)(UN +IN )+CON =UN +(IN +CON )=UN +IN +CON (associatività)
Matrice delle differenze E IN (questa azione è applicabile solo a matrici della stessa dimensione) è detta matrice C della stessa dimensione, i cui elementi sono uguali alla differenza dei corrispondenti elementi della matrice UN E IN .
Trasporre. Se gli elementi di ciascuna riga di una matrice di dimensioni sono scritti nello stesso ordine nelle colonne della nuova matrice, e il numero di colonna è uguale al numero di riga, allora la nuova matrice si dice trasposta rispetto a ed è denotato. La dimensione è La transizione da a si chiama trasposizione. È anche chiaro che. 
, 
Moltiplicazione di matrici. L'operazione di moltiplicazione di matrici è possibile solo se il numero di colonne del primo fattore è uguale al numero di righe del secondo. Come risultato della moltiplicazione, otteniamo una matrice il cui numero di righe coincide con il numero di righe del primo fattore e il numero di colonne con il numero di colonne del secondo: 
Regola della moltiplicazione delle matrici: per ottenere un elemento dell'esima riga e dell'esima colonna del prodotto di due matrici, è necessario moltiplicare gli elementi dell'esima riga della prima matrice per gli elementi dell'esima colonna della seconda matrice e sommare i prodotti risultanti. In gergo matematico a volte si dice: bisogna moltiplicare l'esima riga della matrice per l'esima colonna della matrice. È chiaro che la riga della prima e la colonna della seconda matrice devono contenere lo stesso numero di elementi.
A differenza di queste operazioni, l'operazione di moltiplicazione matrice-matrice è più difficile da definire. Siano date due matrici UN E IN , e il numero di colonne della prima è pari al numero di righe della seconda: ad esempio, la matrice UN ha dimensione e matrice IN – dimensione. Se
, 
, quindi la matrice delle dimensioni
, dove (i=1,…,m;j=1,…,k)
chiamato prodotto della matrice UN alla matrice IN ed è designato AB .
Proprietà dell'operazione di moltiplicazione di matrici:
1. (AB)C=A(BC)=ABC (associatività)
2. (A+B)C=AC+BC (distributività)
3. A(B+C)=AB+A (distributività)
4. La moltiplicazione di matrici non è commutativa: AB non uguale VA ., se uguali, allora queste matrici si dicono commutative.
Trasformazioni elementari su matrici:
1. Scambia due righe (colonne)
2. Moltiplicare una riga (colonna) per un numero diverso da zero
3. Sommando agli elementi di una riga (colonna) gli elementi di un'altra riga (colonna), moltiplicati per un numero qualsiasi
Lezione 1.2.Determinanti a coefficienti reali. Trovare la matrice inversa.
Riepilogo:Determinanti e loro proprietà. Metodi per il calcolo dei determinanti a coefficienti reali. Trovare la matrice inversa per matrici del terzo ordine.
Il concetto di determinante viene introdotto solo per una matrice quadrata. Determinante - Questo numero, che si trova secondo regole ben definite e si denota con o det UN .
Determinante matrici secondo ordine è così: o
Determinante del terzo ordine il numero si chiama:
.
Per ricordare questa formula ingombrante, esiste la “regola dei triangoli”:
Puoi anche calcolare utilizzando un altro metodo: il metodo di scomposizione per riga o colonna. Introduciamo alcune definizioni:
Minore matrice quadrata UN
è detto determinante della matrice UN
, che si ottiene cancellando la -esima riga e la -esima colonna: ad esempio, per minore - 
.
Complemento algebrico L'elemento del determinante si dice minore, preso con il proprio segno se la somma dei numeri della riga e della colonna in cui si trova l'elemento è pari, e con il segno opposto se la somma dei numeri è dispari: .
Poi: Determinante del terzo ordine è uguale alla somma dei prodotti degli elementi di qualsiasi colonna (riga) per i loro complementi algebrici.
PR: Calcoliamo il determinante: espandendolo negli elementi della prima riga.
Proprietà dei determinanti:
1. Il determinante è uguale a 0 se contiene due righe (colonne) identiche o una riga zero (colonna).
2. Il determinante cambia segno quando due righe (colonne) vengono riorganizzate.
3. Il fattore comune in una riga (in una colonna) può essere eliminato oltre il segno del determinante.
4. Il determinante non cambia se a una riga (colonna) viene aggiunta qualsiasi altra riga (un'altra colonna) moltiplicata per un numero arbitrario.
5. Il determinante non cambia quando la matrice viene trasposta.
6. Il determinante della matrice identità è 1:
7. Il determinante del prodotto delle matrici è uguale al prodotto dei determinanti
Matrice inversa.
La matrice quadrata si chiama non degenerato, se il suo determinante è diverso da zero.
Se, quando si moltiplicano matrici quadrate UN E IN in qualsiasi ordine otteniamo la matrice identità ( AB=BA=E ), quindi la matrice IN è detta matrice inversa della matrice UN ed è indicato con , cioè .
Teorema.Ogni matrice non singolare ha un'inversa.
Algoritmo per trovare la matrice inversa:
Matrice inversa. Una matrice quadrata si dice non singolare se il suo determinante è diverso da zero. Altrimenti si dice degenerato .
L'inverso di una matrice si indica con . Se la matrice inversa esiste, allora è unica e 
Dov'è l'aggiunto (unione), composto da addizioni algebriche j: 
Quindi il determinante della matrice inversa è legato al determinante di questa matrice dalla seguente relazione: . Infatti, 
, da cui segue questa uguaglianza.
Proprietà di una matrice inversa:
1. 
, dove sono matrici quadrate non singolari dello stesso ordine.
3. 
.
4. 
Lezione 1.3.Risoluzione di sistemi di equazioni lineari utilizzando il metodo Cramer, i metodi di Gauss e il calcolo matriciale.
Riepilogo:Metodo di Cramer e metodo di Gauss per la risoluzione di sistemi di equazioni algebriche lineari. Metodo matriciale per la risoluzione di sistemi di equazioni. Rango della matrice. Teorema di Kronecker-Capelli. Sistema fondamentale di soluzioni. Sistemi omogenei ed eterogenei.
Il sistema di equazioni è il seguente:
(*) , dove , - coefficienti, - variabili, viene chiamato sistema di equazioni lineari. Risolvere un sistema di equazioni lineari significa indicare tutte le soluzioni del sistema, cioè tali insiemi di valori di variabili che trasformano le equazioni del sistema in identità. Il sistema di equazioni lineari si chiama.
Il metodo di Cramer si basa sull'uso dei determinanti nella risoluzione di sistemi di equazioni lineari. Ciò accelera notevolmente il processo di soluzione.
Il metodo di Cramer può essere utilizzato per risolvere un sistema di tante equazioni lineari quante sono le incognite in ciascuna equazione. Se il determinante del sistema non è uguale a zero, nella soluzione è possibile utilizzare il metodo di Cramer, ma se è uguale a zero, non è possibile. Inoltre, il metodo di Cramer può essere utilizzato per risolvere sistemi di equazioni lineari che hanno un'unica soluzione.
Definizione. Un determinante composto da coefficienti per incognite è chiamato determinante del sistema e si denota (delta).
Determinanti
si ottengono sostituendo i coefficienti delle incognite corrispondenti con termini liberi:
;
.
Il teorema di Cramer. Se il determinante del sistema è diverso da zero, allora il sistema di equazioni lineari ha un'unica soluzione e l'incognita è uguale al rapporto tra i determinanti. Il denominatore contiene il determinante del sistema e il numeratore contiene il determinante ottenuto dal determinante del sistema sostituendo i coefficienti di questa incognita con termini liberi. Questo teorema vale per un sistema di equazioni lineari di qualsiasi ordine.
Esempio 1. Risolvere un sistema di equazioni lineari:
Secondo Il teorema di Cramer abbiamo:
Quindi, la soluzione del sistema (2):
calcolatrice online, metodo di risoluzione di Cramer.
Tre casi di risoluzione di sistemi di equazioni lineari
Come risulta chiaro da Il teorema di Cramer, quando si risolve un sistema di equazioni lineari, possono verificarsi tre casi:
Primo caso: un sistema di equazioni lineari ha un'unica soluzione
(il sistema è coerente e definito)
Secondo caso: un sistema di equazioni lineari ha un numero infinito di soluzioni
(il sistema è coerente e incerto)
** 
,
quelli. i coefficienti delle incognite e dei termini liberi sono proporzionali.
Terzo caso: il sistema di equazioni lineari non ha soluzioni
(il sistema è incoerente)
Quindi il sistema M equazioni lineari con N chiamate variabili non congiunto, se non ha un'unica soluzione, e giunto, se ha almeno una soluzione. Viene chiamato un sistema simultaneo di equazioni che ha una sola soluzione certo, e più di uno – incerto.
Esempi di risoluzione di sistemi di equazioni lineari utilizzando il metodo Cramer
Lasciamo che il sistema sia dato
.
Basato sul teorema di Cramer
………….
,
Dove 
-
determinante del sistema. Otteniamo i restanti determinanti sostituendo la colonna con i coefficienti della corrispondente variabile (sconosciuta) con termini liberi:
Esempio 2.
.
Pertanto il sistema è definito. Per trovare la sua soluzione, calcoliamo i determinanti
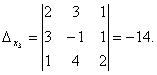
Utilizzando le formule di Cramer troviamo:
Quindi (1; 0; -1) è l'unica soluzione del sistema.
Per verificare le soluzioni dei sistemi di equazioni 3 X 3 e 4 X 4, puoi utilizzare un calcolatore online utilizzando il metodo di risoluzione di Cramer.
Se in un sistema di equazioni lineari non ci sono variabili in una o più equazioni, allora nel determinante gli elementi corrispondenti sono uguali a zero! Questo è il prossimo esempio.
Esempio 3. Risolvi un sistema di equazioni lineari utilizzando il metodo Cramer:
.
Soluzione. Troviamo il determinante del sistema:
Osserva attentamente il sistema di equazioni e il determinante del sistema e ripeti la risposta alla domanda in quali casi uno o più elementi del determinante sono uguali a zero. Quindi il determinante non è uguale a zero, quindi il sistema è definito. Per trovare la sua soluzione, calcoliamo i determinanti per le incognite
Utilizzando le formule di Cramer troviamo:
Quindi la soluzione del sistema è (2; -1; 1).
Per verificare le soluzioni dei sistemi di equazioni 3 X 3 e 4 X 4, puoi utilizzare un calcolatore online utilizzando il metodo di risoluzione di Cramer.
Inizio pagina
Continuiamo a risolvere insieme i sistemi utilizzando il metodo di Cramer
Come già accennato, se il determinante del sistema è uguale a zero, e i determinanti delle incognite non sono uguali a zero, il sistema è incoerente, cioè non ha soluzioni. Illustriamolo con il seguente esempio.
Esempio 6. Risolvi un sistema di equazioni lineari utilizzando il metodo Cramer:
Soluzione. Troviamo il determinante del sistema:
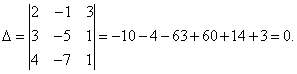
Il determinante del sistema è uguale a zero, quindi il sistema di equazioni lineari è o incoerente e definito, oppure incoerente, cioè non ha soluzioni. Per chiarire, calcoliamo i determinanti per le incognite
Le determinanti delle incognite non sono uguali a zero, quindi il sistema è incoerente, cioè non ha soluzioni.
Per verificare le soluzioni dei sistemi di equazioni 3 X 3 e 4 X 4, puoi utilizzare un calcolatore online utilizzando il metodo di risoluzione di Cramer.
Nei problemi che coinvolgono sistemi di equazioni lineari, ci sono anche quelli in cui, oltre alle lettere che indicano le variabili, ci sono anche altre lettere. Queste lettere rappresentano un numero, molto spesso reale. In pratica, i problemi di ricerca portano a tali equazioni e sistemi di equazioni proprietà generali qualsiasi fenomeno o oggetto. Cioè, ne hai inventato qualcuno nuovo materiale o un dispositivo, e per descriverne le proprietà, che sono comuni indipendentemente dalla dimensione o dal numero di un'istanza, è necessario risolvere un sistema di equazioni lineari, dove al posto di alcuni coefficienti per le variabili ci sono lettere. Non è necessario cercare lontano gli esempi.
L'esempio seguente riguarda un problema simile, aumenta solo il numero di equazioni, variabili e lettere che denotano un certo numero reale.
Esempio 8. Risolvi un sistema di equazioni lineari utilizzando il metodo Cramer:
Soluzione. Troviamo il determinante del sistema:
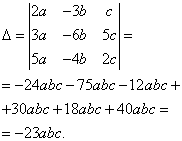
Trovare determinanti per le incognite
Risposta: Il metodo di Cramer si basa sull'uso di determinanti nella risoluzione di sistemi di equazioni lineari. Ciò accelera notevolmente il processo di soluzione.
Definizione. Un determinante composto da coefficienti per incognite è chiamato determinante del sistema e si denota (delta).
Determinanti
si ottengono sostituendo i coefficienti delle incognite corrispondenti con termini liberi:
;
.
Formule di Cramer per trovare le incognite:
.
Trovare i valori di e è possibile solo se
Questa conclusione segue dal seguente teorema.
Il teorema di Cramer. Se il determinante del sistema è diverso da zero, allora il sistema di equazioni lineari ha un'unica soluzione e l'incognita è uguale al rapporto tra i determinanti. Il denominatore contiene il determinante del sistema e il numeratore contiene il determinante ottenuto dal determinante del sistema sostituendo i coefficienti di questa incognita con termini liberi. Questo teorema vale per un sistema di equazioni lineari di qualsiasi ordine.
Esempio 1. Risolvi un sistema di equazioni lineari:
Secondo il teorema di Cramer abbiamo:
Quindi, la soluzione del sistema (2):
9.operazioni sui set. Diagrammi di Vienna.
I diagrammi di Eulero-Venn sono rappresentazioni geometriche di insiemi. La costruzione del diagramma consiste nel disegnare un grande rettangolo che rappresenta l'insieme universale U, e al suo interno - cerchi (o altre figure chiuse) che rappresentano gli insiemi. Le forme devono intersecarsi nel modo più generale richiesto dal problema e devono essere etichettate di conseguenza. I punti che si trovano all'interno di aree diverse del diagramma possono essere considerati come elementi degli insiemi corrispondenti. Una volta costruito il diagramma, puoi ombreggiare determinate aree per indicare i set appena formati.
Le operazioni sugli insiemi vengono considerate per ottenere nuovi insiemi da quelli esistenti.
Definizione. L'unione degli insiemi A e B è un insieme formato da tutti quegli elementi che appartengono ad almeno uno degli insiemi A, B (Fig. 1):
Definizione. L'intersezione degli insiemi A e B è un insieme costituito da tutti quelli e solo quegli elementi che appartengono contemporaneamente sia all'insieme A che all'insieme B (Fig. 2):
Definizione. La differenza tra gli insiemi A e B è l'insieme di tutti quelli e soli elementi di A che non sono contenuti in B (Fig. 3):
Definizione. La differenza simmetrica degli insiemi A e B è l'insieme degli elementi di questi insiemi che appartengono solo all'insieme A o solo all'insieme B (Fig. 4):
11. mappatura (funzione), dominio di definizione, immagini di insiemi durante la mappatura, insieme di valori di una funzione e suo grafico.
Risposta: Una mappatura da un insieme E a un insieme F, o una funzione definita su E con valori in F, è una regola o legge f, che assegna a ciascun elemento un determinato elemento.
Un elemento è chiamato elemento indipendente, o argomento di una funzione f, un elemento è chiamato valore di una funzione f, o immagine; in questo caso, l'elemento è chiamato preimmagine dell'elemento.
Una mappatura (funzione) è solitamente denotata dalla lettera fo dal simbolo, che indica che f mappa l'insieme da E a F. Viene utilizzata anche la notazione, che indica che un elemento x corrisponde a un elemento f(x). A volte è conveniente definire una funzione attraverso un'uguaglianza che contiene una legge di corrispondenza. Ad esempio, si può dire che "la funzione f è definita dall'uguaglianza". Se “y” è il nome generale degli elementi dell’insieme F, cioè F = (y), allora la mappatura si scrive nella forma di uguaglianza y = f(x) e diciamo che questa mappatura è specificata esplicitamente.
2. Immagine e immagine inversa di un insieme sotto una data mappatura
Si diano una mappatura e un insieme.
L'insieme degli elementi di F, ciascuno dei quali è l'immagine di almeno un elemento di D sotto l'applicazione f, è chiamato immagine dell'insieme D ed è indicato con f(D).
Ovviamente, .
Ora sia dato il set.
L'insieme degli elementi tali che , è chiamato immagine inversa dell'insieme Y sotto l'applicazione f ed è indicato con f -1 (Y).
Se, allora. Se per ciascuno l'insieme f -1 (y) consiste di al più un elemento , allora f è detto mappatura biunivoca da E a F. È tuttavia possibile definire una mappatura biunivoca f di l'insieme E su F.
Il display si chiama:
Iniettiva (o iniezione, o mappatura biunivoca dell'insieme E in F) se , oppure se l'equazione f(x) = y ha al più una soluzione;
Suriettiva (o suriezione, o mappatura di un insieme E su F) se f(E) = F e se l'equazione f(x) = y ha almeno una soluzione;
Biiettiva (o biiezione, o mappatura biiettiva di un insieme E su F) se è iniettiva e suriettiva, o se l'equazione f(x) = y ha una ed una sola soluzione.
3. Sovrapposizione di mappature. Mappature inverse, parametriche e implicite
1) Sia e . Poiché , la mappatura g assegna un elemento specifico a ciascun elemento.
Pertanto, ogni elemento viene assegnato tramite una regola
Ciò definisce una nuova mappatura (o una nuova funzione), che chiameremo composizione di mappature, o sovrapposizione di mappature, o mappatura complessa.
2) Sia una mappatura biiettiva e F = (y). Per la biiettività di f, ciascuna corrisponde ad un'immagine unitaria x, che denotiamo con f -1 (y), e tale che f(x) = y. Pertanto, viene definita una mappatura, che viene chiamata l'inverso della mappatura f, o la funzione inversa della funzione f.
Ovviamente, la mappatura f è l'inverso della mappatura f -1 . Pertanto, le mappature f e f -1 sono dette reciprocamente inverse. Per loro valgono le relazioni
e almeno una di queste mappature, ad esempio, è biiettiva. Poi c'è una mappatura inversa, il che significa .
Si dice che una mappatura definita in questo modo sia definita parametricamente utilizzando le mappature; e la variabile da è chiamata parametro.
4) Sia definita una mappatura su un insieme, dove l'insieme contiene l'elemento zero. Supponiamo che esistano insiemi tali che per ogni equazione fissa abbia un'unica soluzione. Allora sull'insieme E è possibile definire una mappatura che assegna a ciascuno il valore che, per un dato x, è soluzione dell'equazione.
Per quanto riguarda la mappatura così definita
si dice che sia dato implicitamente dall'equazione .
5) Una mappatura è chiamata continuazione della mappatura , e g è una restrizione della mappatura f if e .
La restrizione di una mappatura a un insieme è talvolta indicata dal simbolo .
6) Un grafico visualizzato è un insieme
È chiaro che.
12. funzioni monotone. Funzione inversa, teorema di esistenza. Funzioni y=arcsinx y=arcos x x proprietà e grafici.
Risposta: Una funzione monotona è una funzione il cui incremento non cambia segno, cioè è sempre non negativa o sempre non positiva. Se inoltre l'incremento è diverso da zero, la funzione si dice strettamente monotona.
Sia una funzione f(x) definita sull'intervallo
poi lo dicono nel segmento
Notare la differenza tra questa definizione e la definizione di se un segmento è pieno
Di solito, quando si parla di funzione inversa, si sostituisce x con y e y con x(x "y) e si scrive y=f (-1) (x). È ovvio che la funzione originaria f(x) e la funzione inversa f (-1) (x) soddisfano la relazione
f (-1) (f(x))=f(f (-1) (x))=x.
I grafici delle funzioni originaria e inversa sono ottenuti l'uno dall'altro per immagine speculare rispetto alla bisettrice del primo quadrante.
Teorema. Sia definita la funzione f(x), continua e strettamente monotonicamente crescente (decrescente) sull'intervallo. Allora sul segmento viene definita la funzione inversa f (-1) (x), anch'essa continua e che aumenta (diminuisce) rigorosamente monotonicamente.
Prova.
Dimostriamo il teorema per il caso in cui f(x) cresce strettamente monotonicamente.
1. Esistenza di una funzione inversa.
Poiché, per le condizioni del teorema, f(x) è continua, allora, secondo il teorema precedente, il segmento è interamente riempito. Questo significa questo.
Dimostriamo che x è unico. Infatti, se prendiamo x’>x, allora f(x’)>f(x)=y e quindi f(x’)>y. Se prendiamo x'' 2. Monotonicità della funzione inversa. Facciamo la solita sostituzione x «y e scriviamo y= f (-1) (x). Ciò significa che x=f(y). Sia x 1 >x 2 . Poi: y1 = f(-1) (x1); x1 =f(y1) y2 = f(-1) (x2); x2 =f(y2) Qual è la relazione tra y 1 e y 2? Controlliamo le possibili opzioni. a) sì 1 b) y1 =y2? Ma allora f(y 1)=f(y 2) e x 1 =x 2, e avevamo x 1 >x 2. c) L'unica opzione rimasta è y 1 >y 2, cioè Ma allora f (-1) (x 1)>f (-1) (x 2), e questo significa che f (-1) (...) cresce strettamente monotonicamente. 3. Continuità della funzione inversa. Perché i valori della funzione inversa riempiono l'intero segmento, quindi per il teorema precedente f (-1) (...) è continua.< <="" a="" style="color: rgb(255, 68, 0);"> <="" a="" style="color: rgb(0, 0, 0); font-family: Arial; font-size: 11px; font-style: normal; font-variant: normal; font-weight: normal; letter-spacing: normal; line-height: normal; orphans: auto; text-align: start; text-indent: 0px; text-transform: none; white-space: normal; widows: auto; word-spacing: 0px; -webkit-text-stroke-width: 0px; background-color: rgb(0, 171, 160);">
<="" a="" style="color: rgb(255, 68, 0); font-family: Arial; font-size: 11px; font-style: normal; font-variant: normal; font-weight: normal; letter-spacing: normal; line-height: normal; orphans: auto; text-align: start; text-indent: 0px; text-transform: none; white-space: normal; widows: auto; word-spacing: 0px; -webkit-text-stroke-width: 0px; background-color: rgb(0, 171, 160);"> 13.composizione delle funzioni. Funzioni elementari. Funzioni y=arctg x, y = arcctg x, loro proprietà e grafici. Risposta: In matematica, la composizione di funzioni (sovrapposizione di funzioni) è l'applicazione di una funzione al risultato di un'altra. La composizione delle funzioni G e F è solitamente indicata con G∘F, che denota l'applicazione di una funzione G al risultato di una funzione F. Siano F:X→Y e G:F(X)⊂Y→Z due funzioni. Allora la loro composizione è la funzione G∘F:X→Z, definita dall'uguaglianza: (G∘F)(x)=G(F(x)),x∈X. Le funzioni elementari sono funzioni che possono essere ottenute utilizzando un numero finito di operazioni e composizioni aritmetiche dalle seguenti funzioni elementari di base: Ogni funzione elementare può essere specificata da una formula, cioè da un insieme di un numero finito di simboli corrispondenti alle operazioni utilizzate. Tutte le funzioni elementari sono continue nel loro dominio di definizione. A volte le funzioni elementari di base includono anche funzioni iperboliche e iperboliche inverse, sebbene possano essere espresse attraverso le funzioni elementari di base sopra elencate. <="" a="" style="color: rgb(255, 68, 0); font-family: Arial; font-size: 11px; font-style: normal; font-variant: normal; font-weight: normal; letter-spacing: normal; line-height: normal; orphans: auto; text-align: start; text-indent: 0px; text-transform: none; white-space: normal; widows: auto; word-spacing: 0px; -webkit-text-stroke-width: 0px; background-color: rgb(0, 171, 160);">y = arcoseno x y = arco x
funzione inversa della funzione y = sin x, - / 2 x / 2 funzione inversa della funzione y = cos x, 0 x
y = arcotan x y = arco x
funzione inversa della funzione y = tan x, - / 2< x < / 2
funzione inversa alla funzione y = culla x, 0< x <
y > 0 in x R
ESTREMI: NO NO
PROSPETTIVE DELLA MONOTONIA: aumenta con x R diminuisce come x R