Birinin loqarifmi nədir? Loqarifmlərin hesablanması, nümunələr, həllər

Loqarifm nədir?

Diqqət!
Əlavə var
içərisindəki materiallar Xüsusi bölmə 555.
Çox "çox deyil..." olanlar üçün.
Və "çox ..." olanlar üçün)

Loqarifm nədir? Loqarifmləri necə həll etmək olar? Bu suallar bir çox məzunları çaşdırır. Ənənəvi olaraq, loqarifmlər mövzusu mürəkkəb, anlaşılmaz və qorxulu hesab olunur. Xüsusilə - loqarifmli tənliklər.

Bu, qətiyyən doğru deyil. Mütləq! Mənə inanmırsan? Yaxşı. İndi cəmi 10-20 dəqiqə ərzində siz:

1. Anlayacaqsınız loqarifm nədir.

2. Bütün sinfi həll etməyi öyrənin eksponensial tənliklər. Onlar haqqında heç nə eşitməmiş olsanız belə.

3. Sadə loqarifmləri hesablamağı öyrənin.

Üstəlik, bunun üçün sadəcə vurma cədvəlini və ədədi gücə necə yüksəltməyi bilməlisiniz...

Hiss edirəm ki, şübhəniz var... Yaxşı, yaxşı, vaxtı qeyd edin! gedək!

Əvvəlcə bu tənliyi başınızda həll edin:

Bu saytı bəyənirsinizsə...

Yeri gəlmişkən, sizin üçün daha bir neçə maraqlı saytım var.)

Nümunələrin həllində məşq edə və səviyyənizi öyrənə bilərsiniz. Ani yoxlama ilə sınaq. Gəlin öyrənək - maraqla!)

Funksiyalar və törəmələrlə tanış ola bilərsiniz.

Loqarifmin tərifi

b-nin a əsasının loqarifmi b-ni əldə etmək üçün a-nın yüksəldilməli olduğu göstəricidir.

Nömrə e riyaziyyatda ifadənin çalışdığı həddi qeyd etmək adətdir

Nömrə e edir irrasional ədəd - bir ilə müqayisə olunmayan ədəd, onu tam və ya kəsr kimi dəqiq ifadə etmək olmaz rasional nömrə.

Məktub e- ilk hərf Latın sözü ifşa etmək- özünü göstərmək, riyaziyyatda adı belədir eksponensial- eksponensial funksiya.

Nömrə e riyaziyyatda və bu və ya digər şəkildə öz ehtiyacları üçün riyazi hesablamalardan istifadə edən bütün elmlərdə geniş istifadə olunur.

Loqarifmlər. Loqarifmlərin xassələri

Tərif: Loqarifm müsbət rəqəm b əsası c-nin eksponentidir, b ədədini əldə etmək üçün a ədədini qaldırmaq lazımdır.

Əsaslar loqarifmik eynilik:

7) Yeni bazaya keçmək üçün formula:

lna = log e a, e ≈ 2,718…

“Loqarifmlər” mövzusunda məsələlər və testlər. Loqarifmlərin xassələri”

• Loqarifmlər - Riyaziyyatdan Vahid Dövlət İmtahanını nəzərdən keçirmək üçün vacib mövzular

Bu mövzuda tapşırıqları uğurla yerinə yetirmək üçün siz loqarifmin tərifini, loqarifmin xassələrini, əsas loqarifmik eyniliyi, onluq və natural loqarifmlərin təriflərini bilməlisiniz. Bu mövzuya aid məsələlərin əsas növləri loqarifmik ifadələrin hesablanması və çevrilməsi ilə bağlı məsələlərdir. Aşağıdakı nümunələrdən istifadə edərək onların həllini nəzərdən keçirək.

Həlli: Loqarifmlərin xassələrindən istifadə edərək əldə edirik

Həlli: Dərəcələrin xüsusiyyətlərindən istifadə edərək əldə edirik

1) (2 2) log 2 5 =(2 log 2 5) 2 =5 2 =25

Loqarifmlərin xassələri, düsturları və sübutları.

Loqarifmlərin bir sıra var xarakterik xüsusiyyətlər. Bu yazıda əsas şeylərə baxacağıq loqarifmlərin xassələri. Burada onların düsturlarını verəcəyik, loqarifmlərin xassələrini düsturlar şəklində yazacaq, onların tətbiqinə dair nümunələr göstərəcək, həmçinin loqarifmlərin xassələrinin sübutunu təqdim edəcəyik.

Səhifə naviqasiyası.

Loqarifmlərin əsas xassələri, düsturlar

Yadda saxlamaq və istifadə etmək asanlığı üçün təsəvvür edək loqarifmlərin əsas xassələri düsturların siyahısı şəklində. Növbəti bənddə onların tərtibatını, sübutlarını, istifadə nümunələrini və lazımi izahatlarını verəcəyik.

Hissənin loqarifminin xassəsi: , burada a>0, a≠1, x>0, y>0.

Nəticə: , burada a>0, a≠1, n – natural ədəd, birdən böyük, b>0.

Nəticə 1: , a>0 , a≠1 , b>0 , b≠1 .

Nəticə 2: , a>0 , a≠1 , b>0 , p və q həqiqi ədədlərdir, q≠0 , xüsusən b=a üçün bizdə var .

Xassələrin formulları və sübutları

Loqarifmlərin yazılı xassələrinin tərtibinə və sübutuna davam edirik. Loqarifmin bütün xassələri loqarifmin tərifi və ondan irəli gələn əsas loqarifmik eynilik, həmçinin dərəcənin xassələri əsasında sübut edilir.

ilə başlayaq birinin loqarifminin xassələri. Onun tərtibi belədir: birliyin loqarifmi sıfıra bərabərdir, yəni, log a 1=0 hər hansı a>0, a≠1 üçün. Sübut çətin deyil: a>0 və a≠1 yuxarıdakı şərtləri ödəyən hər hansı a üçün a 0 =1 olduğundan, sübut edilməli olan log a 1=0 bərabərliyi dərhal loqarifmin tərifindən irəli gəlir.

Nəzərə alınan xassələrin tətbiqinə dair nümunələr verək: log 3 1=0, log1=0 və .

Növbəti əmlaka keçək: bazaya bərabər olan ədədin loqarifmi birə bərabərdir, yəni, log a a=1 a>0, a≠1 üçün. Həqiqətən, hər hansı a üçün a 1 =a olduğundan, loqarifmin tərifinə görə log a a=1 olur.

Loqarifmlərin bu xassəsinin istifadəsinə misal olaraq log 5 5=1, log 5.6 5.6 və lne=1 bərabərliklərini göstərmək olar.

Loqarifmin əsasına bərabər olan ədədin gücünün loqarifmi eksponentə bərabərdir.. Loqarifmin bu xüsusiyyəti formanın düsturuna uyğundur log a a p =p, burada a>0, a≠1 və p – istənilən real ədəd. Bu xassə birbaşa loqarifmin tərifindən irəli gəlir. Qeyd edək ki, o, loqarifmin dəyərini dərhal göstərməyə imkan verir, əgər loqarifm işarəsi altında olan rəqəmi bazanın gücü kimi təqdim etmək mümkündürsə, bu barədə loqarifmlərin hesablanması məqaləsində daha çox danışacağıq;

Məsələn, log 2 2 7 =7, log10 -4 =-4 və .

İki müsbət ədədin hasilinin loqarifmi x və y bu ədədlərin loqarifmlərinin hasilinə bərabərdir: log a (x y)=log a x+log a y, a>0 , a≠1 . Məhsulun loqarifminin xassəsini sübut edək. Dərəcənin xassələrinə görə a log a x+log a y =a log a x ·a log a y və əsas loqarifmik eyniliyə görə log a x =x və log a y =y olduğundan, log a x ·a log a y olur. =x· y. Beləliklə, log a x+log a y =x·y, ondan loqarifmin tərifi ilə sübut olunan bərabərlik gəlir.

Məhsulun loqarifminin xassəsindən istifadə nümunələrini göstərək: log 5 (2 3)=log 5 2+log 5 3 və .

Məhsulun loqarifminin xassəsi x 1 , x 2 , …, x n müsbət ədədlərinin sonlu n ədədinin hasilinə ümumiləşdirilə bilər. log a (x 1 · x 2 ·…·x n)= log a x 1 +log a x 2 +…+log a x n. Bu bərabərliyi riyazi induksiya metodundan istifadə etməklə problemsiz sübut etmək olar.

Məsələn, hasilin natural loqarifmini 4, e və rəqəmlərinin üç natural loqarifminin cəmi ilə əvəz etmək olar.

İki müsbət ədədin bölünməsinin loqarifmi x və y bu ədədlərin loqarifmləri arasındakı fərqə bərabərdir. Hissənin loqarifminin xassəsi formanın düsturuna uyğundur , burada a>0, a≠1, x və y bəzi müsbət ədədlərdir. Bu düsturun etibarlılığı məhsulun loqarifmi üçün düstur kimi sübut edilmişdir: ildən , sonra loqarifmin tərifi ilə .

Loqarifmin bu xassəsindən istifadə nümunəsi: .

davam edək gücün loqarifminin xassəsi. Dərəcənin loqarifmi bu dərəcənin əsasının eksponentinin və modulunun loqarifmasının hasilinə bərabərdir. Gücün loqarifminin bu xassəsini düstur kimi yazaq: log a b p =p·log a |b|, burada a>0, a≠1, b və p elə ədədlərdir ki, b p dərəcəsi məna verir və b p >0.

Əvvəlcə bu xassəni müsbət b üçün sübut edirik. Əsas loqarifmik eynilik bizə b ədədini log a b , sonra b p =(a log a b) p kimi təqdim etməyə imkan verir və nəticədə yaranan ifadə güc xassəsinə görə p·log a b bərabərdir. Beləliklə, biz b p =a p·log a b bərabərliyinə gəlirik, ondan loqarifmin tərifi ilə belə nəticəyə gəlirik ki, log a b p =p·log a b.

Bu xassəni mənfi b üçün sübut etmək qalır. Burada qeyd edirik ki, mənfi b üçün log a b p ifadəsi yalnız hətta p göstəriciləri üçün məna kəsb edir (çünki b p dərəcəsinin qiyməti sıfırdan böyük olmalıdır, əks halda loqarifmin mənası olmayacaq) və bu halda b p =|b| səh. Sonra b p =|b| p =(a log a |b|) p =a p·log a |b| , haradan log a b p =p·log a |b| .

Məsələn, və ln(-3) 4 =4·ln|-3|=4·ln3 .

Əvvəlki əmlakdan irəli gəlir kökdən loqarifmin xassəsi: n-ci kökün loqarifmi radikal ifadənin loqarifmi ilə 1/n kəsirinin hasilinə bərabərdir, yəni burada a>0, a≠1, n birdən böyük natural ədəddir, b>0 .

Sübut istənilən müsbət b üçün etibarlı olan bərabərliyə (kəsirin eksponentli eksponent tərifinə bax) və eksponentin loqarifminin xassəsinə əsaslanır: .

Bu əmlakdan istifadə nümunəsidir: .

İndi sübut edək yeni loqarifm bazasına keçmək üçün düstur mehriban . Bunun üçün bərabərlik log c b=log a blog·log c a-nın etibarlılığını sübut etmək kifayətdir. Əsas loqarifmik eynilik bizə b ədədini log a b, sonra log c b=log c a log a b kimi təqdim etməyə imkan verir. Dərəcənin loqarifminin xassəsindən istifadə etmək qalır: log c a log a b =log a blo·log c a . Bu log c b=log a b·log c a bərabərliyini sübut edir, yəni loqarifmin yeni bazasına keçid düsturu da sübut edilmişdir. .

Loqarifmlərin bu xassəsindən istifadə etmək üçün bir neçə nümunə göstərək: və .

Yeni bazaya keçmək düsturu sizə “rahat” bazaya malik loqarifmlərlə işləməyə imkan verir. Məsələn, ondan natural və ya onluq loqarifmlərə keçmək üçün istifadə oluna bilər ki, loqarifmin dəyərini loqarifmlər cədvəlindən hesablaya biləsiniz. Yeni loqarifm bazasına keçmək düsturu, bəzi hallarda, bəzi loqarifmlərin digər əsaslarla dəyərləri məlum olduqda, verilmiş loqarifmin dəyərini tapmağa imkan verir.

Formanın c=b üçün yeni loqarifm bazasına keçid formulunun xüsusi halından tez-tez istifadə olunur. Bu göstərir ki, log a b və log b a qarşılıqlı tərs ədədlərdir. Məsələn, .

Düstur da tez-tez istifadə olunur, bu da logarifmlərin dəyərlərini tapmaq üçün əlverişlidir. Sözlərimizi təsdiqləmək üçün formanın loqarifminin dəyərini hesablamaq üçün necə istifadə olunacağını göstərəcəyik. bizdə var . Düsturu sübut etmək üçün a loqarifminin yeni bazasına keçmək üçün düsturdan istifadə etmək kifayətdir: .

Loqarifmlərin müqayisəsinin xüsusiyyətlərini sübut etmək qalır.

Gəlin əks üsuldan istifadə edək. Tutaq ki, 1 >1, a 2 >1 və 1 2 və 0 1 üçün log a 1 b≤log a 2 b doğrudur. Loqarifmlərin xassələrinə əsaslanaraq, bu bərabərsizliklər kimi yenidən yazmaq olar Və müvafiq olaraq və onlardan belə nəticə çıxır ki, müvafiq olaraq log b a 1 ≤log b a 2 və log b a 1 ≥log b a 2. Daha sonra, güclərin xüsusiyyətləri ilə eyni əsaslarla b log b a 1 ≥b log b a 2 və b log b a 1 ≥b log b a 2 bərabərlikləri təmin edilməlidir, yəni a 1 ≥a 2 . Beləliklə, a 1 2 şərti ilə ziddiyyətə gəldik. Bu sübutu tamamlayır.

Loqarifmlərin əsas xassələri

• Dərs üçün materiallar
• Bütün formulları yükləyin

Loqarifmlər, hər hansı bir rəqəm kimi, hər cür əlavə edilə, çıxıla və dəyişdirilə bilər. Lakin loqarifmlər dəqiq olmadığı üçün müntəzəm nömrələr, burada adlanan qaydalar var əsas xassələri.

Siz mütləq bu qaydaları bilməlisiniz - onlarsız heç bir ciddi loqarifmik problem həll edilə bilməz. Bundan əlavə, onlardan çox azdır - bir gündə hər şeyi öyrənə bilərsiniz. Beləliklə, başlayaq.

Loqarifmlərin toplanması və çıxılması

Eyni əsaslara malik iki loqarifmi nəzərdən keçirin: log a x və log a y. Sonra onlar əlavə və çıxıla bilər və:

Deməli, loqarifmlərin cəmi məhsulun loqarifminə, fərqi isə hissənin loqarifmasına bərabərdir. Diqqət yetirin: burada əsas məqam budur eyni əsaslar. Səbəblər fərqlidirsə, bu qaydalar işləmir!

Bu düsturlar hesablamanıza kömək edəcək loqarifmik ifadə hətta onun ayrı-ayrı hissələri hesablanmadıqda belə (“Loqarifm nədir” dərsinə baxın). Nümunələrə nəzər salın və baxın:

Tapşırıq. İfadənin qiymətini tapın: log 6 4 + log 6 9.

Loqarifmlərin əsasları eyni olduğundan, biz cəmi düsturundan istifadə edirik:
log 6 4 + log 6 9 = log 6 (4 9) = log 6 36 = 2.

Tapşırıq. İfadənin qiymətini tapın: log 2 48 − log 2 3.

Əsaslar eynidir, fərq düsturundan istifadə edirik:
log 2 48 − log 2 3 = log 2 (48: 3) = log 2 16 = 4.

Tapşırıq. İfadənin qiymətini tapın: log 3 135 − log 3 5.

Yenə də əsaslar eynidir, buna görə də bizdə:
log 3 135 − log 3 5 = log 3 (135: 5) = log 3 27 = 3.

Göründüyü kimi, orijinal ifadələr ayrıca hesablanmayan “pis” loqarifmlərdən ibarətdir. Amma çevrilmələrdən sonra tam normal ədədlər alınır. Çoxları bu fakt üzərində qurulub testlər. Bəli, Vahid Dövlət İmtahanında test kimi ifadələr bütün ciddiliklə (bəzən faktiki olaraq heç bir dəyişiklik olmadan) təklif olunur.

Loqarifmadan eksponentin çıxarılması

İndi tapşırığı bir az çətinləşdirək. Bəs loqarifmin əsası və ya arqumenti gücdürsə? Sonra bu dərəcənin göstəricisi aşağıdakı qaydalara uyğun olaraq loqarifmin işarəsindən çıxarıla bilər:

• log a x n = n · log a x ;
• 
• 

Sonuncu qaydanın ilk iki qaydaya əməl etdiyini görmək asandır. Ancaq hər halda bunu xatırlamaq daha yaxşıdır - bəzi hallarda hesablamaların miqdarını əhəmiyyətli dərəcədə azaldacaq.

Təbii ki, loqarifmin ODZ-si müşahidə olunarsa, bütün bu qaydalar məna kəsb edir: a > 0, a ≠ 1, x > 0. Və daha bir şey: bütün düsturları yalnız soldan sağa deyil, həm də əksinə tətbiq etməyi öyrənin. , yəni. Loqarifmin özünə loqarifm işarəsindən əvvəlki rəqəmləri daxil edə bilərsiniz. Ən çox tələb olunan budur.

Tapşırıq. İfadənin qiymətini tapın: log 7 49 6 .

Birinci düsturdan istifadə edərək arqumentdəki dərəcədən xilas olaq:
log 7 49 6 = 6 log 7 49 = 6 2 = 12

Tapşırıq. İfadənin mənasını tapın:

[Şəkil üçün başlıq]

Qeyd edək ki, məxrəcdə bazası və arqumenti dəqiq güclər olan loqarifm var: 16 = 2 4 ; 49 = 7 2. Bizdə:

[Şəkil üçün başlıq]

Düşünürəm ki, sonuncu misal müəyyən aydınlaşdırma tələb edir. Loqarifmlər hara getdi? Son ana qədər biz ancaq məxrəclə işləyirik. Orada duran loqarifmin əsasını və arqumentini güclər şəklində təqdim etdik və eksponentləri çıxardıq - "üç mərtəbəli" bir kəsr aldıq.

İndi əsas hissəyə baxaq. Hissənin və məxrəcin eyni ədədi var: log 2 7. log 2 7 ≠ 0 olduğundan kəsri azalda bilərik - 2/4 məxrəcdə qalacaq. Hesab qaydalarına görə, dördü saya köçürmək olar, bu da edilir. Nəticə belə oldu: 2.

Yeni bir təmələ keçid

Loqarifmlərin toplanması və çıxılması qaydaları haqqında danışarkən, onların yalnız eyni əsaslarla işlədiyini xüsusi vurğuladım. Bəs səbəblər fərqlidirsə? Bəs onlar eyni sayda dəqiq səlahiyyətlər deyilsə?

Yeni bir təmələ keçid üçün düsturlar köməyə gəlir. Onları teorem şəklində tərtib edək:

Qoy verilsin loqarifm jurnalı balta. Onda c > 0 və c ≠ 1 olan istənilən c ədədi üçün bərabərlik doğrudur:

[Şəkil üçün başlıq]

Xüsusilə, c = x təyin etsək, alırıq:

[Şəkil üçün başlıq]

İkinci düsturdan belə çıxır ki, loqarifmin əsası və arqumenti dəyişdirilə bilər, lakin bu halda bütün ifadə "çevrilir", yəni. loqarifm məxrəcdə görünür.

Bu düsturlara ənənəvi olaraq nadir hallarda rast gəlinir ədədi ifadələr. Onların nə qədər əlverişli olduğunu yalnız loqarifmik tənliklərin və bərabərsizliklərin həlli zamanı qiymətləndirmək mümkündür.

Ancaq elə problemlər var ki, onları yeni təmələ keçməkdən başqa heç cür həll etmək mümkün deyil. Bunlardan bir neçəsinə baxaq:

Tapşırıq. İfadənin qiymətini tapın: log 5 16 log 2 25.

Qeyd edək ki, hər iki loqarifmin arqumentlərində dəqiq səlahiyyətlər var. Göstəriciləri çıxaraq: log 5 16 = log 5 2 4 = 4log 5 2; log 2 25 = log 2 5 2 = 2log 2 5;

İndi ikinci loqarifmanı “ters” edək:

[Şəkil üçün başlıq]

Faktorları yenidən təşkil edərkən məhsul dəyişmədiyi üçün sakitcə dörd və ikini çoxaltdıq və sonra logarifmlərlə məşğul olduq.

Tapşırıq. İfadənin qiymətini tapın: log 9 100 lg 3.

Birinci loqarifmin əsası və arqumenti dəqiq güclərdir. Bunu yazaq və göstəricilərdən xilas olaq:

[Şəkil üçün başlıq]

İndi yeni bazaya keçərək onluq loqarifmadan xilas olaq:

[Şəkil üçün başlıq]

Əsas loqarifmik eynilik

Çox vaxt həll prosesində ədədi verilmiş bazaya loqarifm kimi təqdim etmək lazımdır. Bu vəziyyətdə aşağıdakı düsturlar bizə kömək edəcəkdir:

1. n = log a a n

2. Birinci halda n ədədi arqumentdə eksponent olur. N rəqəmi tamamilə hər şey ola bilər, çünki bu, sadəcə loqarifm dəyəridir.

   İkinci düstur əslində parafraz tərifdir. Buna belə deyilir: əsas loqarifmik eynilik.

   Əslində, b ədədini elə bir qüvvəyə qaldırsalar ki, bu qüvvəyə verilən b ədədi a rəqəmini versin? Düzdür: nəticə eyni a sayıdır. Bu paraqrafı bir daha diqqətlə oxuyun - bir çox insan ona ilişib qalır.

   Yeni bazaya keçmək üçün düsturlar kimi, əsas loqarifmik eynilik bəzən yeganə mümkün həll yoludur.

   [Şəkil üçün başlıq]

   Qeyd edək ki, log 25 64 = log 5 8 - biz sadəcə olaraq loqarifmin əsasından və arqumentindən kvadrat götürdük. Gücləri eyni baza ilə vurma qaydalarını nəzərə alaraq, alırıq:

   [Şəkil üçün başlıq]

   Kimsə bilmirsə, belə idi əsl problem Vahid Dövlət İmtahanından :)

   Loqarifmik vahid və loqarifmik sıfır

   Yekun olaraq, mən çətin ki, xassələri adlandırmaq mümkün olmayan iki eyniliyi verəcəyəm - daha doğrusu, onlar loqarifmin tərifinin nəticəsidir. Onlar daim problemlər içində görünürlər və təəccüblüdür ki, hətta "qabaqcıl" tələbələr üçün də problemlər yaradırlar.

   1. log a a = 1 loqarifmik vahiddir. Birdəfəlik xatırlayın: bu əsasın özünün hər hansı a əsasının loqarifmi birə bərabərdir.
   2. log a 1 = 0 loqarifmik sıfırdır. a əsası hər hansı bir şey ola bilər, lakin arqumentdə bir varsa, loqarifm sıfıra bərabərdir! Çünki 0 = 1 tərifin birbaşa nəticəsidir.

   Bütün xassələri budur. Onları həyata keçirmək üçün məşq etməyinizə əmin olun! Dərsin əvvəlində fırıldaqçı vərəqini yükləyin, çap edin və problemləri həll edin.

   Loqarifm. Loqarifmin xassələri (toplama və çıxma).

   Loqarifmin xassələri onun tərifindən irəli gəlir. Və beləliklə ədədin loqarifmi bəsasında Aədədin qaldırılmalı olduğu eksponent kimi müəyyən edilir a nömrəni almaq üçün b(loqarifm yalnız müsbət ədədlər üçün mövcuddur).

   Bu formuladan belə çıxır ki, hesablama x=log a b, tənliyin həllinə bərabərdir a x = b. Məsələn, log 2 8 = 3çünki 8 = 2 3 . Loqarifmin tərtibi bunu əsaslandırmağa imkan verir ki, əgər b=a c, sonra ədədin loqarifmi bəsasında a bərabərdir ilə. Loqarifm mövzusunun səlahiyyətlər mövzusu ilə sıx bağlı olduğu da aydındır.

   Loqarifmlərlə, hər hansı bir rəqəmdə olduğu kimi, edə bilərsiniz toplama, çıxma əməliyyatları və hər cür şəkildə dəyişdirin. Lakin loqarifmlərin tamamilə adi ədədlər olmadığı üçün burada öz xüsusi qaydaları tətbiq olunur ki, bunlar da adlanır. əsas xassələri.

   Loqarifmlərin toplanması və çıxılması.

   Eyni əsaslara malik iki loqarifmi götürək: bir x qeyd edin Və log a y. Sonra toplama və çıxma əməliyyatlarını yerinə yetirmək olar:

   Gördüyümüz kimi, loqarifmlərin cəmi məhsulun loqarifminə bərabərdir və fərq loqarifmlər- hissənin loqarifmi. Üstəlik bu rəqəmlər doğrudur A, X Və saat müsbət və a ≠ 1.

   Qeyd etmək lazımdır ki, bu düsturlarda əsas cəhət eyni əsaslardır. Əgər əsaslar fərqlidirsə, bu qaydalar tətbiq edilmir!

   Eyni əsaslı loqarifmlərin toplanması və çıxılması qaydaları yalnız soldan sağa deyil, həm də əksinə oxunur. Nəticədə məhsulun loqarifmi və hissənin loqarifmi üçün teoremlərimiz var.

   Məhsulun loqarifmi iki müsbət ədəd məbləğinə bərabərdir onların loqarifmləri ; bu teoremi izah edərək, rəqəmlər olarsa, aşağıdakıları alırıq A, x Və saat müsbət və a ≠ 1, Bu:

   Hissənin loqarifmi iki müsbət ədəd dividend və bölən loqarifmləri arasındakı fərqə bərabərdir. Başqa cür desək, rəqəmlər A, X Və saat müsbət və a ≠ 1, Bu:

   Həll etmək üçün yuxarıdakı teoremləri tətbiq edək misallar:

   Əgər rəqəmlər x Və saat deməli mənfidir məhsulun loqarifm düsturu mənasız olur. Beləliklə, yazmaq qadağandır:

   log 2 (-8) və log 2 (-4) ifadələri ümumiyyətlə təyin olunmadığından (loqarifmik funksiya) saat= log 2 X yalnız müsbət arqument dəyərləri üçün müəyyən edilir X).

   Məhsul teoremi təkcə iki deyil, həm də qeyri-məhdud sayda amillər üçün tətbiq edilir. Bu o deməkdir ki, hər bir təbii üçün k və istənilən müsbət ədədlər x 1 , x 2 , . . . ,x n bir şəxsiyyət var:

   From loqarifm bölgü teoremi Loqarifmin daha bir xassəsini əldə etmək olar. Qeyd etmək hamıya məlumdur a 1= 0, buna görə də

   Bu o deməkdir ki, bərabərlik var:

   İki əks ədədin loqarifmləri eyni səbəbdən bir-birindən yalnız işarə ilə fərqlənəcək. Beləliklə:

   Loqarifm. Loqarifmlərin xassələri

   Loqarifm. Loqarifmlərin xassələri

   Gəlin bərabərliyi nəzərdən keçirək. Bizə və dəyərlərini bildirin və biz dəyərini tapmaq istəyirik.

   Yəni, biz onu əldə etmək üçün vurmalı olduğumuz eksponenti axtarırıq.

   Qoy dəyişən istənilən real qiymət ala bilər, onda dəyişənlərə aşağıdakı məhdudiyyətlər qoyulur: o" title="a>o"/> , 1″ title="a1″/>, 0" title="b>0" />

   Əgər və -nin dəyərlərini biliriksə və naməlumu tapmaq vəzifəsi ilə qarşılaşırıqsa, bu məqsədlə təqdim edirik. riyazi əməliyyat adlanır loqarifm.

   Aldığımız dəyəri tapmaq üçün ədədin loqarifmi By əsas :

   Ədədin bazasına olan loqarifmi, onu almaq üçün qaldırılmalı olduğu göstəricidir.

   Yəni əsas loqarifmik eynilik:

   o» title=»a>o»/> , 1″ title=»a1″/>, 0″ title=»b>0″/>

   mahiyyətcə riyazi qeyddir loqarifmin tərifləri.

   Loqarifmin riyazi əməliyyatı eksponentasiya əməliyyatının tərsidir, deməli loqarifmlərin xassələri dərəcə xassələri ilə sıx bağlıdır.

   Əsasını sadalayaq loqarifmlərin xassələri:

   (o" title="a>o"/> , 1″ title=»a1″/>, 0″ title=»b>0″/>, 0,

   d>0″/>, 1″ başlıq=”d1″/>

   4.

   5.

   Aşağıdakı xüsusiyyətlər qrupu loqarifmin işarəsi altında və ya loqarifmin əsasında dayanan ifadənin eksponentini loqarifmin işarəsinin qarşısında əmsal şəklində təmsil etməyə imkan verir:

   6.

   7.

   8.

   9.

   Növbəti düsturlar qrupu verilmiş əsaslı loqarifmadan ixtiyari əsaslı loqarifmaya keçməyə imkan verir və adlanır. yeni bazaya keçmək üçün düsturlar:

   10.

   12. (11-ci əmlakdan nəticə)

   

   Aşağıdakı üç xüsusiyyət yaxşı məlum deyil, lakin onlar tez-tez loqarifmik tənlikləri həll edərkən və ya loqarifmləri ehtiva edən ifadələri sadələşdirərkən istifadə olunur:

   13.

   14.

   15.

   Xüsusi hallar:

   — onluq loqarifm

   — təbii loqarifm

   Loqarifmləri ehtiva edən ifadələri sadələşdirərkən ümumi bir yanaşma istifadə olunur:

   1. Təqdim etmək ondalıklar adi olanlar şəklində.

   2. Qarışıq ədədləri düzgün olmayan kəsrlər kimi təqdim edirik.

   3. Loqarifmin əsasında və işarəsi altında olan ədədləri sadə amillərə parçalayırıq.

   4. Bütün loqarifmləri eyni bazaya endirməyə çalışırıq.

   5. Loqarifmlərin xassələrini tətbiq edin.

   Loqarifmləri ehtiva edən ifadələrin sadələşdirilməsinə dair nümunələrə baxaq.

   Misal 1.

   Hesablayın:

   Gəlin bütün göstəriciləri sadələşdirək: bizim vəzifəmiz onları bazası eksponentin əsası ilə eyni ədəd olan loqarifmlərə endirməkdir.

   ==(xassəyə görə 7)=(xassəyə görə 6) =

   Gəlin əldə etdiyimiz göstəriciləri orijinal ifadə ilə əvəz edək. Biz əldə edirik:

   Cavab: 5.25

   Misal 2. Hesablayın:

   

   Bütün loqarifmləri 6-cı bazaya endirək (bu halda kəsrin məxrəcindən loqarifmlər saya “köçəcək”):

   Loqarifm işarəsi altındakı ədədləri sadə amillərə parçalayaq:

   4 və 6 xassələri tətbiq edək:

   Əvəzedicini təqdim edək

   Biz əldə edirik:

   Cavab: 1

   Loqarifm . Əsas loqarifmik eynilik.

   Loqarifmlərin xassələri. Ondalıq loqarifm. Təbii loqarifm.

   Loqarifm bazaya müsbət N ədədi (b > 0, b 1) N əldə etmək üçün b-nin qaldırılmalı olduğu x göstəricisidir .

   Bu giriş aşağıdakılara bərabərdir: b x = N .

   Nümunələr: log 3 81 = 4, çünki 3 4 = 81;

   log 1/3 27 = – 3, çünki (1/3) - 3 = 3 3 = 27.

   Loqarifmin yuxarıdakı tərifi eynilik kimi yazıla bilər:

   

   Loqarifmlərin əsas xassələri.

   2) log 1 = 0, çünki b 0 = 1 .

   3) Məhsulun loqarifmi amillərin loqarifmlərinin cəminə bərabərdir:

   4) Bölmənin loqarifmi dividend və bölən loqarifmləri arasındakı fərqə bərabərdir:

   5) Gücün loqarifmi eksponentin və onun əsasının loqarifminin hasilinə bərabərdir:

   Bu əmlakın nəticəsi aşağıdakılardır: kökün loqarifmi kökün gücünə bölünən radikal ədədin loqarifminə bərabərdir:

   

   6) Loqarifmin əsası dərəcədirsə, onda qiymət eksponentin tərsini log qafiyəsi kimi çıxarmaq olar:

   

   Son iki xüsusiyyət birinə birləşdirilə bilər:

   

   7) Keçid modulu düsturu (yəni bir loqarifm bazasından digər bazaya keçid):

   

   Xüsusi halda, nə vaxt N=a bizdə:

   

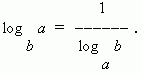
   Ondalıq loqarifm çağırdı əsas loqarifm 10. lg təyin olunur, yəni. log 10 N= log N. 10, 100, 1000, ədədlərinin loqarifmləri. p müvafiq olaraq 1, 2, 3, …, yəni. çox müsbət var

   vahidlər, loqarifmik ədəddə birdən sonra neçə sıfır var. 0.1, 0.01, 0.001, ədədlərinin loqarifmləri. p müvafiq olaraq –1, –2, –3, …, yəni. loqarifmik ədəddə birdən əvvəl sıfırların sayı qədər mənfi olanlar (sıfır tam ədədlər daxil olmaqla). Digər ədədlərin loqarifmləri adlı kəsr hissəsi var mantis. Bütün hissə loqarifm deyilir xarakterik. Praktik istifadə üçün onluq loqarifmlər ən əlverişlidir.

   Təbii loqarifm çağırdı əsas loqarifm e. ln ilə işarələnir, yəni. log e N= log N. Nömrə e irrasionaldır, onun təxmini dəyəri 2,718281828-dir. Bu rəqəmin meyl etdiyi hədddir (1 + 1 / n) n limitsiz artımla n(sm. birinci gözəl hədd "Limitlər" səhifəsində nömrə ardıcıllığı»).
   Nə qədər qəribə görünsə də, təbii loqarifmlər funksiyaların təhlili ilə bağlı müxtəlif növ əməliyyatları yerinə yetirərkən çox əlverişli oldu. Loqarifmlərin bazaya hesablanması e hər hansı digər səbəbdən çox daha sürətli həyata keçirilir.

• Rusiyada uşağı övladlığa götürmək üçün bu gün nə lazımdır? Rusiyada övladlığa götürmə, məsuliyyətli şəxsi qərara əlavə olaraq, namizədlərin dövlət tərəfindən yoxlanılması üçün bir sıra prosedurları əhatə edir. Hazırlıq mərhələsində ciddi seçim daha çox kömək edir [...]
• Rusiya daxilində vergi reyestrindən VÖEN və ya OGRN haqqında pulsuz məlumat - dövlət qeydiyyatı haqqında məlumat Vahid Vergi Xidmətləri Portalında əldə edilə bilər hüquqi şəxslər, fərdi sahibkarlar, […]
• Sənədsiz maşın sürməyə görə cəza (sürücülük vəsiqəsi, sığorta, STS) Bəzən unutqanlıq ucbatından sürücülər vəsiqəsiz sükan arxasına keçirlər və sənədsiz maşın sürdüklərinə görə cərimə də alırlar. Xatırladaq ki, avtomobil həvəskarı özü ilə birlikdə hərəkət edir məcburi […]
• Kişilər üçün çiçəklər. Bir kişiyə hansı çiçəkləri verə bilərsiniz? Bir kişiyə hansı çiçəkləri verə bilərsiniz? Çox "kişi" çiçəklər yoxdur, lakin kişilərə verilən bəziləri var. Qarşınızda kiçik bir çiçək siyahısı: Xrizantema.
• Güllər. Qərənfillər.
• […]
• Xidmət qeydi müəssisənin daxili mühitində istifadə olunan və cari istehsal problemlərinin operativ həllinə xidmət edən xüsusi sənəd formasıdır. Adətən bu sənəd bəzi […] Sberbank-dan pensiyanızın maliyyələşdirilən hissəsini nə vaxt və necə almaq olar? Sberbank dövlət pensiya fondunun tərəfdaş bankıdır. Buna əsaslanaraq, yığılan pensiya üçün qeydiyyatdan keçmiş vətəndaşlar yığılan hissəni köçürə bilər [...]
• Ulyanovskda uşaq müavinətləri və Ulyanovsk rayonu 2018-ci ildə Bundan əlavə, bütün subyektlər federal qanunvericiliklə təsdiq edilmiş proqramları fəaliyyət göstərir. Gəlin baxaq, kim hansı faydalara arxalana bilər. Regional hakimiyyət orqanları necə […]Ətraflı Bələdçi