Qual è il logaritmo di uno? Calcolo dei logaritmi, esempi, soluzioni

Cos'è un logaritmo?

Attenzione!
Ce ne sono altri
materiali dentro Parte speciale 555.
Per coloro che sono molto "non molto..."
E per chi “tantissimo…”)

Cos'è un logaritmo? Come risolvere i logaritmi? Queste domande confondono molti laureati. Tradizionalmente, il tema dei logaritmi è considerato complesso, incomprensibile e spaventoso. Particolarmente - equazioni con logaritmi.

Questo non è assolutamente vero. Assolutamente! Non mi credi? Bene. Ora, in soli 10 - 20 minuti:

1. Comprendi cos'è un logaritmo.

2. Impara a risolvere un'intera classe equazioni esponenziali. Anche se non ne hai sentito parlare.

3. Impara a calcolare semplici logaritmi.

Inoltre, per questo ti basterà conoscere la tavola pitagorica e come elevare un numero a potenza...

Mi sembra che tu abbia dei dubbi... Beh, okay, prenditi il ​​tempo! Andiamo!

Innanzitutto, risolvi questa equazione nella tua testa:

Se ti piace questo sito...

A proposito, ho un paio di altri siti interessanti per te.)

Puoi esercitarti a risolvere esempi e scoprire il tuo livello. Test con verifica immediata. Impariamo - con interesse!)

Puoi familiarizzare con funzioni e derivate.

Definizione di logaritmo

Il logaritmo di b in base a è l'esponente al quale deve essere elevato a per ottenere b.

Numero e in matematica è consuetudine denotare il limite al quale tende un'espressione

Numero eÈ numero irrazionale - un numero incommensurabile con uno, non può essere espresso con precisione né come numero intero né come frazione razionale numero.

Lettera e- prima lettera Parola latina esponente- mettersi in mostra, da qui il nome in matematica esponenziale- funzione esponenziale.

Numero e ampiamente utilizzato in matematica, e in tutte le scienze che in un modo o nell'altro utilizzano i calcoli matematici per le loro esigenze.

Logaritmi. Proprietà dei logaritmi

Definizione: logaritmo numero positivo La base b è l'esponente di c al quale bisogna elevare il numero a per ottenere il numero b.

Nozioni di base identità logaritmica:

7) Formula per trasferirsi in una nuova base:

lna = log e a, e ≈ 2.718…

Problemi e prove sul tema “Logaritmi. Proprietà dei logaritmi"

• Logaritmi - Argomenti importanti per il ripasso dell'Esame di Stato Unificato di matematica

Per completare con successo le attività su questo argomento, è necessario conoscere la definizione di logaritmo, le proprietà dei logaritmi, l'identità logaritmica di base, le definizioni di logaritmi decimali e naturali. I principali tipi di problemi su questo argomento sono problemi che coinvolgono il calcolo e la trasformazione di espressioni logaritmiche. Consideriamo la loro soluzione utilizzando i seguenti esempi.

Soluzione: Usando le proprietà dei logaritmi, otteniamo

Soluzione: Usando le proprietà dei gradi, otteniamo

1) (2 2) log 2 5 =(2 log 2 5) 2 =5 2 =25

Proprietà dei logaritmi, formulazioni e dimostrazioni.

I logaritmi hanno un numero di proprietà caratteristiche. In questo articolo vedremo i principali proprietà dei logaritmi. Qui forniremo le loro formulazioni, annoteremo le proprietà dei logaritmi sotto forma di formule, mostreremo esempi della loro applicazione e forniremo anche prove delle proprietà dei logaritmi.

Navigazione della pagina.

Proprietà fondamentali dei logaritmi, formule

Per facilità di memorizzazione e utilizzo, immaginiamo proprietà fondamentali dei logaritmi sotto forma di un elenco di formule. Nel paragrafo successivo ne daremo le formulazioni, le testimonianze, gli esempi di utilizzo e le necessarie spiegazioni.

Proprietà del logaritmo dell'unità: log a 1=0 per ogni a>0, a≠1.

Logaritmo di un numero, uguale alla base: log a a=1 per a>0, a≠1.

Proprietà del logaritmo della potenza della base: log a a p = p, dove a>0, a≠1 e p è un numero reale qualsiasi.

Logaritmo del prodotto di due numeri positivi: log a (x y)=log a x+log a y , a>0 , a≠1 , x>0 , y>0 ,
e la proprietà del logaritmo del prodotto di n numeri positivi: log a (x 1 · x 2 ·…·x n)= log a x 1 +log a x 2 +…+log a x n , a>0 , a≠1 , x 1 >0, x 2 >0, …, x n >0 .

Proprietà del logaritmo di un quoziente: , dove a>0, a≠1, x>0, y>0.

Logaritmo della potenza di un numero: log a b p = p·log a |b| , dove a>0, a≠1, b e p sono numeri tali che il grado b p abbia senso e b p >0.

Conseguenza: , dove a>0, a≠1, n – numero naturale, maggiore di uno, b>0.

Corollario 1: , a>0 , a≠1 , b>0 , b≠1 .

Corollario 2: , a>0 , a≠1 , b>0 , p e q sono numeri reali, q≠0 , in particolare per b=a abbiamo .

Formulazioni e prove di proprietà

Procediamo alla formulazione e alla dimostrazione delle proprietà scritte dei logaritmi. Tutte le proprietà dei logaritmi sono dimostrate in base alla definizione del logaritmo e all'identità logaritmica di base che ne consegue, nonché alle proprietà del grado.

Cominciamo con proprietà del logaritmo di uno. La sua formulazione è la seguente: il logaritmo dell'unità è uguale a zero, cioè registra un 1=0 per ogni a>0, a≠1. La dimostrazione non è difficile: poiché a 0 =1 per ogni a che soddisfa le condizioni di cui sopra a>0 e a≠1, allora il log di uguaglianza a 1=0 da dimostrare segue immediatamente dalla definizione del logaritmo.

Diamo esempi di applicazione della proprietà considerata: log 3 1=0, log1=0 e .

Passiamo alla proprietà successiva: il logaritmo di un numero uguale alla base è uguale a uno, questo è, log a a=1 per a>0, a≠1. Infatti, poiché a 1 =a per qualsiasi a, allora per definizione del logaritmo log a a=1.

Esempi di utilizzo di questa proprietà dei logaritmi sono le uguaglianze log 5 5=1, log 5.6 5.6 e lne=1.

Il logaritmo di una potenza di un numero uguale alla base del logaritmo è uguale all'esponente. Questa proprietà del logaritmo corrisponde a una formula della forma log a a p = p, dove a>0, a≠1 e p – qualsiasi numero reale. Questa proprietà deriva direttamente dalla definizione di logaritmo. Da notare che permette di indicare subito il valore del logaritmo, se è possibile rappresentare il numero sotto il segno del logaritmo come una potenza della base ne parleremo più approfonditamente nell'articolo Calcolo dei logaritmi;

Ad esempio, log 2 2 7 =7, log10 -4 =-4 e .

Logaritmo del prodotto di due numeri positivi xey è uguale al prodotto dei logaritmi di questi numeri: log a (x y)=log a x+log a y, a>0 , a≠1 . Dimostriamo la proprietà del logaritmo di un prodotto. A causa delle proprietà del grado a log a x+log a y =a log a x ·a log a y, e poiché per l'identità logaritmica principale a log a x =x e a log a y =y, allora a log a x ·a log a y =x·y. Quindi, un log a x+log a y =x·y, da cui, per la definizione di logaritmo, segue l'uguaglianza da dimostrare.

Mostriamo esempi di utilizzo della proprietà del logaritmo di un prodotto: log 5 (2 3)=log 5 2+log 5 3 e .

La proprietà del logaritmo di un prodotto può essere generalizzata al prodotto di un numero finito n di numeri positivi x 1 , x 2 , …, x n come log a (x 1 · x 2 ·…·x n)= log a x 1 +log a x 2 +…+log a x n. Questa uguaglianza può essere dimostrata senza problemi utilizzando il metodo dell'induzione matematica.

Ad esempio, il logaritmo naturale del prodotto può essere sostituito dalla somma di tre logaritmi naturali dei numeri 4, e, e.

Logaritmo del quoziente di due numeri positivi xey è uguale alla differenza tra i logaritmi di questi numeri. La proprietà del logaritmo di un quoziente corrisponde a una formula della forma , dove a>0, a≠1, xey sono alcuni numeri positivi. La validità di questa formula è dimostrata così come quella della formula per il logaritmo di un prodotto: poiché , quindi per definizione di logaritmo .

Ecco un esempio di utilizzo di questa proprietà del logaritmo: .

Passiamo a proprietà del logaritmo della potenza. Il logaritmo di un grado è uguale al prodotto dell'esponente e del logaritmo del modulo della base di questo grado. Scriviamo questa proprietà del logaritmo di una potenza come formula: log a b p =p·log a |b|, dove a>0, a≠1, b e p sono numeri tali che il grado b p abbia senso e b p >0.

Per prima cosa dimostriamo questa proprietà per il positivo b. L'identità logaritmica di base ci permette di rappresentare il numero b come un log a b , quindi b p =(a log a b) p , e l'espressione risultante, per la proprietà della potenza, è uguale a a p·log a b . Arriviamo così all'uguaglianza b p = a p·log a b, da cui, per la definizione di logaritmo, concludiamo che log a b p = p·log a b.

Resta da dimostrare questa proprietà per b negativo. Qui notiamo che l'espressione log a b p per b negativo ha senso solo per esponenti pari p (poiché il valore del grado b p deve essere maggiore di zero, altrimenti il ​​logaritmo non avrà senso), e in questo caso b p =|b| P. Allora bp =|b| p =(a log a |b|) p =a p·log a |b| , da dove log a b p = p·log a |b| .

Per esempio, e ln(-3) 4 =4·ln|-3|=4·ln3 .

Ne consegue dalla proprietà precedente proprietà del logaritmo dalla radice: il logaritmo della radice n-esima è uguale al prodotto della frazione 1/n per il logaritmo dell'espressione radicale, cioè dove a>0, a≠1, n è un numero naturale maggiore di uno, b>0 .

La dimostrazione si basa sull'uguaglianza (vedi definizione di esponente con esponente frazionario), valida per qualsiasi b positivo, e sulla proprietà del logaritmo dell'esponente: .

Ecco un esempio di utilizzo di questa proprietà: .

Ora dimostriamo formula per passare a una nuova base logaritmica Tipo . Per fare ciò è sufficiente dimostrare la validità dell'uguaglianza log c b=log a b·log c a. L'identità logaritmica di base ci consente di rappresentare il numero b come log a b , quindi log c b=log c a log a b . Resta da utilizzare la proprietà del logaritmo del grado: log c a log a b =log a b·log c a . Ciò dimostra l'uguaglianza log c b=log a b·log c a, il che significa che è dimostrata anche la formula per la transizione a una nuova base del logaritmo .

Mostriamo un paio di esempi di utilizzo di questa proprietà dei logaritmi: e .

La formula per passare a una nuova base ti consente di passare a lavorare con logaritmi che hanno una base “conveniente”. Ad esempio, può essere utilizzato per passare ai logaritmi naturali o decimali in modo da poter calcolare il valore di un logaritmo da una tabella di logaritmi. La formula per passare ad una nuova base logaritmica consente anche, in alcuni casi, di trovare il valore di un dato logaritmo quando si conoscono i valori di alcuni logaritmi con altre basi.

Viene spesso utilizzato un caso speciale della formula per la transizione a una nuova base logaritmica per c=b della forma. Ciò dimostra che log a b e log b a sono numeri reciprocamente inversi. Per esempio, .

Spesso viene utilizzata anche la formula, utile per trovare i valori dei logaritmi. Per confermare le nostre parole, mostreremo come può essere utilizzato per calcolare il valore di un logaritmo della forma . Abbiamo . Per dimostrare la formula è sufficiente utilizzare la formula per passare a una nuova base del logaritmo a: .

Resta da dimostrare le proprietà di confronto dei logaritmi.

Usiamo il metodo opposto. Supponiamo che per a 1 >1, a 2 >1 e a 1 2 e per 0 1, log a 1 b≤log a 2 b sia vero. Sulla base delle proprietà dei logaritmi, queste disuguaglianze possono essere riscritte come E rispettivamente, e da essi segue che log b a 1 ≤ log b a 2 e log b a 1 ≥ log b a 2, rispettivamente. Quindi, dalle proprietà dei poteri con per gli stessi motivi devono essere soddisfatte le uguaglianze b log b a 1 ≥b log b a 2 e b log b a 1 ≥b log b a 2, cioè a 1 ≥a 2 . Quindi siamo arrivati ​​a una contraddizione con la condizione a 1 2. Questo completa la dimostrazione.

Proprietà fondamentali dei logaritmi

• Materiali per la lezione
• Scarica tutte le formule

I logaritmi, come qualsiasi numero, possono essere aggiunti, sottratti e trasformati in ogni modo. Ma poiché i logaritmi non sono esattamente numeri ordinari, ci sono delle regole qui, che si chiamano principali proprietà.

Devi assolutamente conoscere queste regole: senza di esse non è possibile risolvere un solo problema logaritmico serio. Inoltre, ce ne sono pochissimi: puoi imparare tutto in un giorno. Quindi cominciamo.

Somma e sottrazione di logaritmi

Consideriamo due logaritmi con le stesse basi: log a x e log a y. Quindi possono essere aggiunti e sottratti e:

Quindi, la somma dei logaritmi è uguale al logaritmo del prodotto e la differenza è uguale al logaritmo del quoziente. Nota: il punto chiave qui è motivi identici. Se i motivi sono diversi, queste regole non funzionano!

Queste formule ti aiuteranno a calcolare espressione logaritmica anche quando le sue singole parti non vengono contate (vedi la lezione “Che cos'è un logaritmo”). Dai un'occhiata agli esempi e vedi:

Compito. Trova il valore dell'espressione: log 6 4 + log 6 9.

Poiché i logaritmi hanno le stesse basi, usiamo la formula di somma:
log 6 4 + log 6 9 = log 6 (4 9) = log 6 36 = 2.

Compito. Trova il valore dell'espressione: log 2 48 − log 2 3.

Le basi sono le stesse, usiamo la formula della differenza:
log 2 48 − log 2 3 = log 2 (48: 3) = log 2 16 = 4.

Compito. Trova il valore dell'espressione: log 3 135 − log 3 5.

Anche in questo caso le basi sono le stesse, quindi abbiamo:
log 3 135 − log 3 5 = log 3 (135: 5) = log 3 27 = 3.

Come puoi vedere, le espressioni originali sono composte da logaritmi “cattivi”, che non vengono calcolati separatamente. Ma dopo le trasformazioni si ottengono numeri del tutto normali. Molti si basano su questo fatto test. Sì, le espressioni simili ai test vengono offerte in tutta serietà (a volte praticamente senza modifiche) durante l'Esame di Stato unificato.

Estrarre l'esponente dal logaritmo

Ora complichiamo un po' il compito. Cosa succede se la base o l'argomento di un logaritmo è una potenza? Quindi l'esponente di questo grado può essere estratto dal segno del logaritmo secondo le seguenti regole:

• logaritmo a x n = n · logaritmo a x ;
• 
• 

È facile vedere che l'ultima regola segue le prime due. Ma è comunque meglio ricordarlo: in alcuni casi ridurrà significativamente la quantità di calcoli.

Naturalmente, tutte queste regole hanno senso se si rispetta l'ODZ del logaritmo: a > 0, a ≠ 1, x > 0. E ancora una cosa: impara ad applicare tutte le formule non solo da sinistra a destra, ma anche viceversa , cioè. Puoi inserire i numeri prima del segno del logaritmo nel logaritmo stesso. Questo è ciò che più spesso viene richiesto.

Compito. Trova il valore dell'espressione: log 7 49 6 .

Eliminiamo la laurea nell'argomento utilizzando la prima formula:
logaritmo 7 49 6 = 6 logaritmo 7 49 = 6 2 = 12

Compito. Trova il significato dell'espressione:

[Didascalia dell'immagine]

Nota che il denominatore contiene un logaritmo, la cui base e argomento sono potenze esatte: 16 = 2 4 ; 49 = 72. Abbiamo:

[Didascalia dell'immagine]

Penso che l’ultimo esempio richieda alcuni chiarimenti. Dove sono finiti i logaritmi? Fino all'ultimo momento lavoriamo solo con il denominatore. Abbiamo presentato la base e l'argomento del logaritmo sotto forma di potenze e abbiamo eliminato gli esponenti: abbiamo ottenuto una frazione "a tre piani".

Ora diamo un'occhiata alla frazione principale. Il numeratore e il denominatore contengono lo stesso numero: log 2 7. Poiché log 2 7 ≠ 0, possiamo ridurre la frazione: 2/4 rimarranno nel denominatore. Secondo le regole dell'aritmetica, il quattro può essere trasferito al numeratore, e così è stato fatto. Il risultato è stata la risposta: 2.

Transizione ad una nuova fondazione

Parlando delle regole per aggiungere e sottrarre i logaritmi, ho sottolineato in particolare che funzionano solo con le stesse basi. E se i motivi fossero diversi? E se non fossero potenze esatte dello stesso numero?

Le formule per il passaggio a una nuova fondazione vengono in soccorso. Formuliamoli sotto forma di teorema:

Lascia che sia dato registro dei logaritmi ascia. Quindi per qualsiasi numero c tale che c > 0 e c ≠ 1, l'uguaglianza è vera:

[Didascalia dell'immagine]

In particolare, se poniamo c = x, otteniamo:

[Didascalia dell'immagine]

Dalla seconda formula segue che la base e l'argomento del logaritmo possono essere invertiti, ma in questo caso l'intera espressione viene “capovolta”, cioè il logaritmo appare al denominatore.

Queste formule si trovano raramente in quelle convenzionali espressioni numeriche. È possibile valutare quanto siano convenienti solo quando si risolvono equazioni e disequazioni logaritmiche.

Tuttavia, ci sono problemi che non possono essere risolti se non passando a una nuova fondazione. Diamo un'occhiata ad un paio di questi:

Compito. Trova il valore dell'espressione: log 5 16 log 2 25.

Nota che gli argomenti di entrambi i logaritmi contengono potenze esatte. Togliamo gli indicatori: log 5 16 = log 5 2 4 = 4log 5 2; log 2 25 = log 2 5 2 = 2log 2 5;

Adesso “invertiamo” il secondo logaritmo:

[Didascalia dell'immagine]

Poiché il prodotto non cambia quando si riorganizzano i fattori, abbiamo moltiplicato con calma quattro per due e poi ci siamo occupati dei logaritmi.

Compito. Trova il valore dell'espressione: log 9 100 lg 3.

La base e l'argomento del primo logaritmo sono potenze esatte. Scriviamolo ed eliminiamo gli indicatori:

[Didascalia dell'immagine]

Ora eliminiamo il logaritmo decimale spostandoci su una nuova base:

[Didascalia dell'immagine]

Identità logaritmica di base

Spesso nel processo risolutivo è necessario rappresentare un numero come logaritmo in base data. In questo caso ci aiuteranno le seguenti formule:

1. n = log a a n

2. Nel primo caso, il numero n diventa l'esponente dell'argomento. Il numero n può essere assolutamente qualsiasi cosa, perché è semplicemente un valore logaritmico.

   La seconda formula è in realtà una definizione parafrasata. Si chiama così: identità logaritmica di base.

   Infatti, cosa succede se il numero b viene elevato a una potenza tale che il numero b a questa potenza dà il numero a? Esatto: il risultato è lo stesso numero a. Leggi di nuovo attentamente questo paragrafo: molte persone rimangono bloccate.

   Come le formule per passare a una nuova base, l'identità logaritmica di base è talvolta l'unica soluzione possibile.

   [Didascalia dell'immagine]

   Nota che log 25 64 = log 5 8 - abbiamo semplicemente preso il quadrato dalla base e dall'argomento del logaritmo. Tenendo conto delle regole per moltiplicare le potenze con la stessa base, otteniamo:

   [Didascalia dell'immagine]

   Se qualcuno non lo sa, lo era vera sfida dall'Esame di Stato Unificato :)

   Unità logaritmica e zero logaritmico

   In conclusione, darò due identità che difficilmente possono essere chiamate proprietà, ma piuttosto sono conseguenze della definizione del logaritmo. Appaiono costantemente nei problemi e, sorprendentemente, creano problemi anche agli studenti “avanzati”.

   1. log a a = 1 è un'unità logaritmica. Ricorda una volta per tutte: il logaritmo di qualsiasi base a di quella base stessa è uguale a uno.
   2. log a 1 = 0 è zero logaritmico. La base a può essere qualsiasi cosa, ma se l'argomento ne contiene uno, il logaritmo è uguale a zero! Perché a 0 = 1 è una conseguenza diretta della definizione.

   Queste sono tutte le proprietà. Assicurati di esercitarti a metterli in pratica! Scarica il cheat sheet all'inizio della lezione, stampalo e risolvi i problemi.

   Logaritmo. Proprietà del logaritmo (addizione e sottrazione).

   Proprietà del logaritmo derivare dalla sua definizione. E quindi il logaritmo del numero B basato su UNè definito come l'esponente a cui deve essere elevato un numero UN per ottenere il numero B(il logaritmo esiste solo per i numeri positivi).

   Da questa formulazione consegue che il calcolo x=log a b, equivale a risolvere l'equazione ax=b. Per esempio, log28 = 3 Perché 8 = 2 3 . La formulazione del logaritmo permette di giustificare che se b=un c, quindi il logaritmo del numero B basato su UNè uguale Con. È anche chiaro che il tema dei logaritmi è strettamente correlato al tema delle potenze.

   Con i logaritmi, come con qualsiasi numero, puoi farlo operazioni di addizione, sottrazione e trasformarlo in ogni modo possibile. Ma poiché i logaritmi non sono numeri del tutto ordinari, qui si applicano le loro regole speciali, che vengono chiamate principali proprietà.

   Somma e sottrazione di logaritmi.

   Prendiamo due logaritmi con le stesse basi: registra un x E registra un anno. Successivamente è possibile eseguire operazioni di addizione e sottrazione:

   Come vediamo, somma dei logaritmiè uguale al logaritmo del prodotto e differenza logaritmi- logaritmo del quoziente. Inoltre, questo è vero se i numeri UN, X E A positivo e un ≠ 1.

   È importante notare che l'aspetto principale di queste formule sono le stesse basi. Se i motivi sono diversi, queste regole non si applicano!

   Le regole per aggiungere e sottrarre logaritmi con le stesse basi vengono lette non solo da sinistra a destra, ma anche viceversa. Di conseguenza, abbiamo i teoremi per il logaritmo del prodotto e il logaritmo del quoziente.

   Logaritmo del prodotto due numeri positivi pari alla somma i loro logaritmi ; parafrasando questo teorema otteniamo quanto segue se i numeri UN, X E A positivo e un ≠ 1, Quello:

   Logaritmo del quoziente due numeri positivi equivalgono alla differenza tra i logaritmi del dividendo e del divisore. Per dirla in altro modo, se i numeri UN, X E A positivo e un ≠ 1, Quello:

   Applichiamo i teoremi precedenti per risolvere esempi:

   Se i numeri X E A sono negativi, quindi formula del logaritmo del prodotto diventa privo di significato. Pertanto è vietato scrivere:

   poiché le espressioni log 2 (-8) e log 2 (-4) non sono affatto definite (funzione logaritmica A= log2 X definito solo per valori di argomenti positivi X).

   Teorema del prodotto applicabile non solo per due, ma anche per un numero illimitato di fattori. Ciò significa che per ogni naturale k e tutti i numeri positivi X 1 , X 2 , . . . ,x n c'è un'identità:

   Da Teorema del quoziente logaritmico si può ottenere un'altra proprietà del logaritmo. È risaputo che log UN 1= 0, quindi

   Ciò significa che esiste un'uguaglianza:

   Logaritmi di due numeri reciproci per lo stesso motivo differiranno tra loro unicamente per il segno. COSÌ:

   Logaritmo. Proprietà dei logaritmi

   Logaritmo. Proprietà dei logaritmi

   Consideriamo l'uguaglianza. Facci sapere i valori di e e vogliamo trovare il valore di .

   Cioè, stiamo cercando l'esponente con cui dobbiamo armarlo per ottenere .

   Permettere una variabile può assumere qualsiasi valore reale, alle variabili vengono imposte le seguenti restrizioni: o" title="a>o"/> , 1″ title="a1″/>, 0″ title="b>0″ />

   Se conosciamo i valori di e e ci troviamo di fronte al compito di trovare l'ignoto, allora a questo scopo introduciamo operazione matematica che si chiama logaritmo.

   Per trovare il valore prendiamo logaritmo di un numero Di base :

   Il logaritmo di un numero alla sua base è l'esponente a cui deve essere elevato per ottenere .

   Questo è identità logaritmica di base:

   o» title=»a>o»/> , 1″ title=»a1″/>, 0″ title=»b>0″/>

   è essenzialmente una notazione matematica definizioni di logaritmo.

   L'operazione matematica del logaritmo è l'inverso dell'operazione di esponenziazione, quindi proprietà dei logaritmi sono strettamente legati alle proprietà del grado.

   Elenchiamo i principali proprietà dei logaritmi:

   (o" title="a>o"/> , 1″ title=»a1″/>, 0″ title=»b>0″/>, 0,

   d>0″/>, 1″ titolo="d1″/>

   4.

   5.

   Il seguente gruppo di proprietà permette di rappresentare l'esponente di un'espressione sotto il segno del logaritmo, oppure alla base del logaritmo come coefficiente davanti al segno del logaritmo:

   6.

   7.

   8.

   9.

   Il successivo gruppo di formule permette di passare da un logaritmo con base data a un logaritmo con base arbitraria, e si chiama formule per la transizione ad una nuova base:

   10.

   12. (corollario della proprietà 11)

   

   Le seguenti tre proprietà non sono ben note, ma vengono spesso utilizzate quando si risolvono equazioni logaritmiche o quando si semplificano espressioni contenenti logaritmi:

   13.

   14.

   15.

   Casi particolari:

   — logaritmo decimale

   — logaritmo naturale

   Quando si semplificano le espressioni contenenti logaritmi, viene utilizzato un approccio generale:

   1. Presentazione decimali sotto forma di quelli ordinari.

   2. Rappresentiamo i numeri misti come frazioni improprie.

   3. Scomponiamo i numeri alla base del logaritmo e sotto il segno del logaritmo in fattori semplici.

   4. Cerchiamo di ridurre tutti i logaritmi alla stessa base.

   5. Applicare le proprietà dei logaritmi.

   Diamo un'occhiata ad esempi di semplificazione di espressioni contenenti logaritmi.

   Esempio 1.

   Calcolare:

   Semplifichiamo tutti gli esponenti: il nostro compito è ridurli a logaritmi, la cui base è uguale alla base dell'esponente.

   ==(per proprietà 7)=(per proprietà 6) =

   Sostituiamo gli indicatori che abbiamo inserito nell'espressione originale. Otteniamo:

   Risposta: 5.25

   Esempio 2. Calcola:

   

   Riduciamo tutti i logaritmi in base 6 (in questo caso, i logaritmi dal denominatore della frazione “migreranno” al numeratore):

   Scomponiamo i numeri sotto il segno del logaritmo in fattori semplici:

   Applichiamo le proprietà 4 e 6:

   Presentiamo la sostituzione

   Otteniamo:

   Risposta: 1

   Logaritmo . Identità logaritmica di base.

   Proprietà dei logaritmi. Logaritmo decimale. Logaritmo naturale.

   Logaritmo numero positivo N in base (B > 0, B 1) è l'esponente x al quale bisogna elevare b per ottenere N .

   Questa voce è equivalente alla seguente: bx = N .

   Esempi: log 3 81 = 4, poiché 3 4 = 81;

   ceppo 1/3 27 = – 3, poiché (1/3) - 3 = 3 3 = 27.

   La definizione di logaritmo sopra può essere scritta come un'identità:

   

   Proprietà fondamentali dei logaritmi.

   2) log 1 = 0, poiché B 0 = 1 .

   3) Il logaritmo del prodotto è uguale alla somma dei logaritmi dei fattori:

   4) Il logaritmo del quoziente è uguale alla differenza tra i logaritmi del dividendo e del divisore:

   5) Il logaritmo di una potenza è uguale al prodotto dell'esponente per il logaritmo della sua base:

   La conseguenza di questa proprietà è la seguente: logaritmo della radice uguale al logaritmo del numero radicale diviso per la potenza della radice:

   

   6) Se la base del logaritmo è un grado, allora il valore l'inverso dell'esponente può essere estratto come una rima logaritmica:

   

   Le ultime due proprietà possono essere combinate in una sola:

   

   7) Formula del modulo di transizione (cioè transizione da una base logaritmica a un'altra base):

   

   Nel caso speciale quando N=d abbiamo:

   

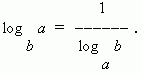
   Logaritmo decimale chiamato logaritmo di base 10. È indicato con lg, cioè registro 10 N= registro N. Logaritmi dei numeri 10, 100, 1000, . p sono 1, 2, 3, …, rispettivamente, cioè ne ho tanti di positivi

   unità, quanti zeri ci sono in un numero logaritmico dopo l'uno. Logaritmi dei numeri 0.1, 0.01, 0.001, . p sono rispettivamente –1, –2, –3, …, cioè avere tanti negativi quanti sono gli zeri nel numero logaritmico prima dell'uno (inclusi gli zero interi). I logaritmi degli altri numeri hanno una parte frazionaria chiamata mantissa. Parte intera si chiama il logaritmo caratteristica. Per l'uso pratico, i logaritmi decimali sono i più convenienti.

   Logaritmo naturale chiamato logaritmo di base e. È indicato con ln, cioè tronco d'albero e N= registro N. Numero eè irrazionale, il suo valore approssimativo è 2,718281828. È il limite a cui tende il numero (1+1/ N) N con incremento illimitato N(cm. Primo limite meraviglioso nella pagina "Limiti". sequenze numeriche»).
   Per quanto strano possa sembrare, i logaritmi naturali si sono rivelati molto convenienti quando si eseguono vari tipi di operazioni legate all'analisi delle funzioni. Calcolo dei logaritmi in base e effettuato molto più velocemente che per qualsiasi altro motivo.

• Cosa serve oggi per adottare un bambino in Russia? L'adozione in Russia, oltre a una decisione personale responsabile, comporta una serie di procedure per la verifica statale dei candidati. Una selezione rigorosa nella fase preparatoria contribuisce a […]
• Informazioni gratuite su TIN o OGRN dal registro fiscale in tutta la Russia - online Le informazioni sulla registrazione statale possono essere ottenute sul portale dei servizi fiscali unificati persone giuridiche, singoli imprenditori, […]
• Punizione per guida senza documenti (patente, assicurazione, STS) A volte, per dimenticanza, i conducenti si mettono al volante senza patente e ricevono una multa per guida senza documenti. Ricordiamo che l'appassionato di auto guida con la sua obbligatorio […]
• Fiori per uomini. Quali fiori puoi regalare a un uomo? Quali fiori puoi regalare a un uomo? Non ci sono molti fiori “maschili”, ma ce ne sono alcuni che vengono regalati agli uomini. Una piccola lista di fiori davanti a te: Crisantemi.
• Rose. Garofani.
• […]
• Nota di servizio è una forma speciale di documento che viene utilizzata nell'ambiente interno di un'impresa e serve a risolvere rapidamente gli attuali problemi di produzione. Tipicamente questo documento viene redatto con lo scopo di introdurre alcuni […] Quando e come ricevere la parte finanziata della pensione da Sberbank? Sberbank è una banca partner del fondo pensione statale. Sulla base di ciò, i cittadini che si sono registrati per una pensione finanziata potrebbero trasferire la parte finanziata […]
• Assegni familiari a Ulyanovsk e Regione di Ul'janovsk nel 2018 Inoltre, tutti i soggetti gestiscono programmi approvati dalla legislazione federale. Diamo un'occhiata a chi può contare su quali vantaggi. Come le autorità regionali […] Guida dettagliata