Menu
Secara percuma
Pendaftaran
Rumah  /  Pelepasan/ Apakah logaritma bagi satu. Pengiraan logaritma, contoh, penyelesaian

Apakah logaritma bagi satu? Pengiraan logaritma, contoh, penyelesaian

Apakah logaritma?

Perhatian!
Ada tambahan
bahan dalam Seksyen khas 555.
Bagi mereka yang sangat "tidak sangat..."
Dan bagi mereka yang “sangat…”)

Apakah logaritma? Bagaimana untuk menyelesaikan logaritma? Soalan-soalan ini mengelirukan ramai graduan. Secara tradisinya, topik logaritma dianggap kompleks, tidak dapat difahami dan menakutkan. Terutamanya - persamaan dengan logaritma.

Ini sama sekali tidak benar. Sudah tentu! Tidak percaya saya? baiklah. Kini, hanya dalam 10 - 20 minit anda:

1. Anda akan faham apa itu logaritma.

2. Belajar menyelesaikan keseluruhan kelas persamaan eksponen. Walaupun anda tidak pernah mendengar apa-apa tentang mereka.

3. Belajar mengira logaritma mudah.

Selain itu, untuk ini anda hanya perlu mengetahui jadual pendaraban dan cara menaikkan nombor kepada kuasa...

Saya rasa awak ada keraguan... Baik, okey, tandakan masanya! jom pergi!

Pertama, selesaikan persamaan ini di kepala anda:

Jika anda suka laman web ini...

By the way, saya ada beberapa lagi tapak yang menarik untuk anda.)

Anda boleh berlatih menyelesaikan contoh dan mengetahui tahap anda. Menguji dengan pengesahan segera. Mari belajar - dengan minat!)

Anda boleh berkenalan dengan fungsi dan derivatif.

Definisi logaritma

Logaritma b kepada asas a ialah eksponen yang a mesti dinaikkan untuk mendapatkan b.

Nombor e dalam matematik adalah kebiasaan untuk menyatakan had yang diusahakan oleh ungkapan

Nombor e ialah nombor tak rasional - nombor yang tidak boleh dibandingkan dengan satu, ia tidak boleh dinyatakan dengan tepat sama ada sebagai integer atau pecahan rasional nombor.

surat e- huruf pertama perkataan Latin exponere- untuk menunjuk-nunjuk, maka namanya dalam matematik eksponen- fungsi eksponen.

Nombor e digunakan secara meluas dalam matematik, dan dalam semua sains yang dalam satu cara atau yang lain menggunakan pengiraan matematik untuk keperluan mereka.

Logaritma. Sifat logaritma

Definisi: Logaritma nombor positif Asas b ialah eksponen bagi c yang mana nombor a mesti dinaikkan untuk mendapatkan nombor b.

Asas identiti logaritma:

7) Formula untuk berpindah ke pangkalan baharu:

lna = log e a, e ≈ 2.718…

Masalah dan ujian mengenai topik "Logaritma. Sifat logaritma"

  • Logaritma - Topik penting untuk menyemak Peperiksaan Negeri Bersepadu dalam matematik

Untuk berjaya menyelesaikan tugasan mengenai topik ini, anda mesti mengetahui takrifan logaritma, sifat-sifat logaritma, identiti logaritma asas, takrifan logaritma perpuluhan dan asli. Jenis masalah utama mengenai topik ini ialah masalah yang melibatkan pengiraan dan transformasi ungkapan logaritma. Mari kita pertimbangkan penyelesaian mereka menggunakan contoh berikut.

Penyelesaian: Menggunakan sifat logaritma, kita dapat

Penyelesaian: Menggunakan sifat darjah, kita dapat

1) (2 2) log 2 5 =(2 log 2 5) 2 =5 2 =25

Sifat logaritma, rumusan dan bukti.

Logaritma mempunyai beberapa sifat ciri. Dalam artikel ini kita akan melihat perkara utama sifat logaritma. Di sini kami akan memberikan rumusan mereka, menulis sifat logaritma dalam bentuk formula, menunjukkan contoh aplikasinya, dan juga memberikan bukti sifat logaritma.

Navigasi halaman.

Sifat asas logaritma, formula

Untuk kemudahan mengingat dan menggunakannya, mari kita bayangkan sifat asas logaritma dalam bentuk senarai formula. Dalam perenggan seterusnya kami akan memberikan rumusan, bukti, contoh penggunaan dan penjelasan yang diperlukan.

  • Sifat logaritma perpaduan: log a 1=0 untuk sebarang a>0, a≠1.
  • Logaritma nombor, sama dengan asas: log a a=1 untuk a>0, a≠1.
  • Sifat logaritma kuasa tapak: log a a p =p, dengan a>0, a≠1 dan p ialah sebarang nombor nyata.
  • Logaritma hasil darab dua nombor positif: log a (x y)=log a x+log a y , a>0 , a≠1 , x>0 , y>0 ,
    dan sifat logaritma hasil darab n nombor positif: log a (x 1 · x 2 ·…·x n)= log a x 1 +log a x 2 +…+log a x n , a>0 , a≠1 , x 1 >0, x 2 >0, …, x n >0 .
  • Sifat logaritma hasil bagi: , di mana a>0, a≠1, x>0, y>0.
  • Logaritma kuasa nombor: log a b p =p·log a |b| , di mana a>0, a≠1, b dan p ialah nombor sedemikian rupa sehingga darjah b p masuk akal dan b p >0.
  • Akibat: , di mana a>0, a≠1, n – nombor asli, lebih besar daripada satu, b>0.
  • Akibat 1: , a>0 , a≠1 , b>0 , b≠1 .
  • Akibat 2: , a>0 , a≠1 , b>0 , p dan q ialah nombor nyata, q≠0 , khususnya untuk b=a yang kita ada .

    • Formulasi dan bukti sifat

    Kami meneruskan ke perumusan dan pembuktian sifat bertulis logaritma. Semua sifat logaritma dibuktikan berdasarkan takrifan logaritma dan identiti logaritma asas yang mengikuti daripadanya, serta sifat darjah.

    Mari kita mulakan dengan sifat logaritma satu. Perumusannya adalah seperti berikut: logaritma perpaduan adalah sama dengan sifar, iaitu, log a 1=0 untuk sebarang a>0, a≠1. Buktinya tidak sukar: kerana a 0 =1 untuk mana-mana a memenuhi syarat di atas a>0 dan a≠1, maka log kesamaan a 1=0 yang akan dibuktikan mengikuti serta-merta daripada takrifan logaritma.

    Mari kita berikan contoh aplikasi harta yang dipertimbangkan: log 3 1=0, log1=0 dan .

    Mari kita beralih ke harta seterusnya: logaritma nombor yang sama dengan asas adalah sama dengan satu, iaitu, log a a=1 untuk a>0, a≠1. Sesungguhnya, oleh kerana a 1 =a untuk sebarang a, maka mengikut takrifan logaritma log a a=1.

    Contoh penggunaan sifat logaritma ini ialah kesamaan log 5 5=1, log 5.6 5.6 dan lne=1.

    Logaritma kuasa nombor yang sama dengan asas logaritma adalah sama dengan eksponen. Sifat logaritma ini sepadan dengan formula bentuk log a a p =p, dengan a>0, a≠1 dan p – sebarang nombor nyata. Sifat ini mengikuti terus daripada takrifan logaritma. Ambil perhatian bahawa ia membolehkan anda untuk segera menunjukkan nilai logaritma, jika mungkin untuk mewakili nombor di bawah tanda logaritma sebagai kuasa asas, kita akan bercakap lebih lanjut mengenai perkara ini dalam artikel mengira logaritma.

    Contohnya, log 2 2 7 =7, log10 -4 =-4 dan .

    Logaritma hasil darab dua nombor positif x dan y adalah sama dengan hasil darab logaritma nombor ini: log a (x y)=log a x+log a y, a>0 , a≠1 . Mari kita buktikan sifat logaritma produk. Disebabkan oleh sifat darjah a log a x+log a y =a log a x ·a log a y, dan oleh kerana oleh identiti logaritma utama log a x =x dan log a y =y, maka log a x ·a log a y =x· y. Oleh itu, log a x+log a y =x·y, daripadanya, mengikut takrifan logaritma, kesamaan yang dibuktikan berikut.

    Mari tunjukkan contoh menggunakan sifat logaritma hasil darab: log 5 (2 3)=log 5 2+log 5 3 dan .

    Sifat logaritma hasil darab boleh digeneralisasikan kepada hasil darab nombor terhingga n nombor positif x 1 , x 2 , …, x n sebagai log a (x 1 · x 2 ·…·x n)= log a x 1 +log a x 2 +…+log a x n. Kesamaan ini boleh dibuktikan tanpa masalah menggunakan kaedah aruhan matematik.

    Sebagai contoh, logaritma asli produk boleh digantikan dengan hasil tambah tiga logaritma asli bagi nombor 4, e, dan.

    Logaritma hasil bagi dua nombor positif x dan y adalah sama dengan perbezaan antara logaritma nombor ini. Sifat logaritma hasil bagi sepadan dengan formula bentuk , dengan a>0, a≠1, x dan y ialah beberapa nombor positif. Kesahihan formula ini terbukti serta formula untuk logaritma produk: sejak , kemudian mengikut takrifan logaritma .

    Berikut ialah contoh menggunakan sifat logaritma ini: .

    Mari kita beralih kepada sifat logaritma kuasa. Logaritma darjah adalah sama dengan hasil darab eksponen dan logaritma modulus asas darjah ini. Mari kita tulis sifat logaritma kuasa ini sebagai formula: log a b p =p·log a |b|, di mana a>0, a≠1, b dan p ialah nombor sedemikian rupa sehingga darjah b p masuk akal dan b p >0.

    Mula-mula kita buktikan sifat ini untuk positif b. Identiti logaritma asas membolehkan kita mewakili nombor b sebagai log a b , kemudian b p =(a log a b) p , dan ungkapan yang terhasil, disebabkan oleh sifat kuasa, adalah sama dengan p·log a b . Jadi kita sampai kepada kesamaan b p =a p·log a b, dari mana, mengikut takrifan logaritma, kita membuat kesimpulan bahawa log a b p =p·log a b.

    Ia kekal untuk membuktikan sifat ini untuk negatif b. Di sini kita perhatikan bahawa ungkapan log a b p untuk negatif b masuk akal hanya untuk eksponen genap p (kerana nilai darjah b p mestilah lebih besar daripada sifar, jika tidak logaritma tidak akan masuk akal), dan dalam kes ini b p =|b| hlm. Kemudian b p ==b| p =(a log a |b|) p =a p·log a |b| , dari mana log a b p =p·log a |b| .

    Sebagai contoh, dan ln(-3) 4 =4·ln|-3|=4·ln3 .

    Ia mengikuti dari harta sebelumnya sifat logaritma daripada punca: logaritma punca ke-n adalah sama dengan hasil darab pecahan 1/n dengan logaritma ungkapan radikal, iaitu, di mana a>0, a≠1, n ialah nombor asli lebih besar daripada satu, b>0 .

    Buktinya adalah berdasarkan kesamaan (lihat takrifan eksponen dengan eksponen pecahan), yang sah untuk sebarang b positif, dan sifat logaritma eksponen: .

    Berikut ialah contoh menggunakan harta ini: .

    Sekarang mari kita buktikan formula untuk berpindah ke asas logaritma baharu baik hati . Untuk melakukan ini, sudah cukup untuk membuktikan kesahihan log kesamaan c b=log a b·log c a. Identiti logaritma asas membolehkan kita mewakili nombor b sebagai log a b , kemudian log c b=log c a log a b . Ia kekal menggunakan sifat logaritma darjah: log c a log a b =log a b·log c a . Ini membuktikan log kesamaan c b=log a b·log c a, yang bermaksud formula peralihan kepada asas baharu logaritma juga terbukti .

    Mari tunjukkan beberapa contoh menggunakan sifat logaritma ini: dan .

    Formula untuk berpindah ke pangkalan baharu membolehkan anda meneruskan kerja dengan logaritma yang mempunyai asas "mudah". Sebagai contoh, ia boleh digunakan untuk menukar kepada logaritma semula jadi atau perpuluhan supaya anda boleh mengira nilai logaritma daripada jadual logaritma. Formula untuk berpindah ke asas logaritma baharu juga membenarkan, dalam beberapa kes, untuk mencari nilai logaritma tertentu apabila nilai beberapa logaritma dengan asas lain diketahui.

    Kes khas formula untuk peralihan kepada asas logaritma baru untuk c=b bentuk sering digunakan. Ini menunjukkan bahawa log a b dan log b a adalah nombor songsang. Sebagai contoh, .

    Formula ini juga sering digunakan, yang mudah untuk mencari nilai logaritma. Untuk mengesahkan perkataan kami, kami akan menunjukkan cara ia boleh digunakan untuk mengira nilai logaritma borang . Kami ada . Untuk membuktikan formula, cukup menggunakan formula untuk berpindah ke asas baru logaritma a: .

    Ia kekal untuk membuktikan sifat-sifat perbandingan logaritma.

    Mari gunakan kaedah yang bertentangan. Katakan untuk a 1 >1, a 2 >1 dan a 1 2 dan untuk 0 1, log a 1 b≤log a 2 b adalah benar. Berdasarkan sifat logaritma, ketaksamaan ini boleh ditulis semula sebagai Dan masing-masing, dan daripada mereka ia mengikuti bahawa log b a 1 ≤log b a 2 dan log b a 1 ≥log b a 2, masing-masing. Kemudian, dengan sifat-sifat kuasa dengan atas alasan yang sama kesamaan b log b a 1 ≥b log b a 2 dan b log b a 1 ≥b log b a 2 mesti dipenuhi, iaitu a 1 ≥a 2 . Jadi kami sampai kepada percanggahan dengan syarat a 1 2. Ini melengkapkan bukti.

    Sifat asas logaritma

    • Bahan untuk pelajaran
    • Muat turun semua formula

      • Logaritma, seperti mana-mana nombor, boleh ditambah, ditolak dan diubah dalam semua cara. Tetapi kerana logaritma tidak tepat nombor biasa, terdapat peraturan di sini, yang dipanggil sifat utama.

      Anda pastinya perlu mengetahui peraturan ini - tanpanya satu masalah logaritma yang serius tidak dapat diselesaikan. Di samping itu, terdapat sangat sedikit daripada mereka - anda boleh mempelajari segala-galanya dalam satu hari. Jadi mari kita mulakan.

      Menambah dan menolak logaritma

      Pertimbangkan dua logaritma dengan asas yang sama: log a x dan log a y. Kemudian mereka boleh ditambah dan ditolak, dan:

      Jadi, jumlah logaritma adalah sama dengan logaritma hasil darab, dan perbezaannya adalah sama dengan logaritma hasil bagi. Sila ambil perhatian: perkara utama di sini ialah alasan yang sama. Jika alasannya berbeza, peraturan ini tidak berfungsi!

      Formula ini akan membantu anda mengira ungkapan logaritma walaupun bahagian individunya tidak dikira (lihat pelajaran “Apakah itu logaritma”). Lihat contoh dan lihat:

      Tugasan. Cari nilai ungkapan: log 6 4 + log 6 9.

      Oleh kerana logaritma mempunyai asas yang sama, kami menggunakan formula jumlah:
      log 6 4 + log 6 9 = log 6 (4 9) = log 6 36 = 2.

      Tugasan. Cari nilai ungkapan: log 2 48 − log 2 3.

      Asasnya adalah sama, kami menggunakan formula perbezaan:
      log 2 48 − log 2 3 = log 2 (48: 3) = log 2 16 = 4.

      Tugasan. Cari nilai ungkapan: log 3 135 − log 3 5.

      Sekali lagi pangkalannya adalah sama, jadi kami mempunyai:
      log 3 135 − log 3 5 = log 3 (135: 5) = log 3 27 = 3.

      Seperti yang anda lihat, ungkapan asal terdiri daripada logaritma "buruk", yang tidak dikira secara berasingan. Tetapi selepas transformasi, nombor normal sepenuhnya diperolehi. Banyak yang dibina atas fakta ini ujian. Ya, ungkapan seperti ujian ditawarkan dalam semua kesungguhan (kadangkala hampir tiada perubahan) pada Peperiksaan Negeri Bersepadu.

      Mengeluarkan eksponen daripada logaritma

      Sekarang mari kita merumitkan sedikit tugas. Bagaimana jika asas atau hujah logaritma ialah kuasa? Kemudian eksponen darjah ini boleh dikeluarkan dari tanda logaritma mengikut peraturan berikut:

    • log a x n = n · log a x ;

      • Adalah mudah untuk melihat bahawa peraturan terakhir mengikuti dua yang pertama. Tetapi lebih baik untuk mengingatinya - dalam beberapa kes ia akan mengurangkan jumlah pengiraan dengan ketara.

      Sudah tentu, semua peraturan ini masuk akal jika ODZ logaritma diperhatikan: a > 0, a ≠ 1, x > 0. Dan satu lagi perkara: belajar menggunakan semua formula bukan sahaja dari kiri ke kanan, tetapi juga sebaliknya , iaitu Anda boleh memasukkan nombor sebelum logaritma masuk ke dalam logaritma itu sendiri. Inilah yang paling kerap diperlukan.

      Tugasan. Cari nilai ungkapan: log 7 49 6 .

      Mari kita buang darjah dalam hujah menggunakan formula pertama:
      log 7 49 6 = 6 log 7 49 = 6 2 = 12

      Tugasan. Cari maksud ungkapan:

      [Kapsyen untuk gambar]

      Perhatikan bahawa penyebutnya mengandungi logaritma, asas dan hujahnya adalah kuasa tepat: 16 = 2 4 ; 49 = 7 2. Kami ada:

      [Kapsyen untuk gambar]

      Saya rasa contoh terakhir memerlukan beberapa penjelasan. Ke mana perginya logaritma? Sehingga saat terakhir kita bekerja hanya dengan penyebut. Kami membentangkan asas dan hujah logaritma yang berdiri di sana dalam bentuk kuasa dan mengeluarkan eksponen - kami mendapat pecahan "tiga tingkat".

      Sekarang mari kita lihat pecahan utama. Pengangka dan penyebut mengandungi nombor yang sama: log 2 7. Oleh kerana log 2 7 ≠ 0, kita boleh mengurangkan pecahan - 2/4 akan kekal dalam penyebut. Mengikut peraturan aritmetik, empat boleh dipindahkan ke pengangka, iaitu apa yang telah dilakukan. Hasilnya ialah jawapan: 2.

      Peralihan kepada asas baharu

      Bercakap tentang peraturan untuk menambah dan menolak logaritma, saya secara khusus menekankan bahawa ia hanya berfungsi dengan asas yang sama. Bagaimana jika sebabnya berbeza? Bagaimana jika mereka bukan kuasa tepat nombor yang sama?

      Formula untuk peralihan kepada asas baharu datang untuk menyelamatkan. Mari kita rumuskan dalam bentuk teorem:

      Biarlah diberi log logaritma kapak. Kemudian untuk sebarang nombor c supaya c > 0 dan c ≠ 1, kesamaan adalah benar:

      [Kapsyen untuk gambar]

      Khususnya, jika kita menetapkan c = x, kita mendapat:

      [Kapsyen untuk gambar]

      Daripada formula kedua ia mengikuti bahawa asas dan hujah logaritma boleh ditukar, tetapi dalam kes ini keseluruhan ungkapan "terbalik", i.e. logaritma muncul dalam penyebut.

      Formula ini jarang ditemui dalam konvensional ungkapan berangka. Adalah mungkin untuk menilai betapa mudahnya mereka hanya apabila menyelesaikan persamaan logaritma dan ketaksamaan.

      Namun, terdapat masalah yang tidak dapat diselesaikan sama sekali kecuali dengan berpindah ke asas baru. Mari kita lihat beberapa perkara ini:

      Tugasan. Cari nilai ungkapan: log 5 16 log 2 25.

      Ambil perhatian bahawa hujah kedua-dua logaritma mengandungi kuasa yang tepat. Mari kita keluarkan penunjuk: log 5 16 = log 5 2 4 = 4log 5 2; log 2 25 = log 2 5 2 = 2log 2 5;

      Sekarang mari kita "terbalikkan" logaritma kedua:

      [Kapsyen untuk gambar]

      Memandangkan produk tidak berubah apabila menyusun semula faktor, kami dengan tenang mendarab empat dan dua, dan kemudian berurusan dengan logaritma.

      Tugasan. Cari nilai ungkapan: log 9 100 lg 3.

      Asas dan hujah logaritma pertama adalah kuasa yang tepat. Mari kita tulis ini dan singkirkan penunjuk:

      [Kapsyen untuk gambar]

      Sekarang mari kita buang logaritma perpuluhan dengan berpindah ke pangkalan baharu:

      [Kapsyen untuk gambar]

      Identiti logaritma asas

      Selalunya dalam proses penyelesaian adalah perlu untuk mewakili nombor sebagai logaritma kepada asas tertentu. Dalam kes ini, formula berikut akan membantu kami:

    1. n = log a a n

    2. Dalam kes pertama, nombor n menjadi eksponen dalam hujah. Nombor n boleh menjadi apa-apa sahaja, kerana ia hanyalah nilai logaritma.

      Formula kedua sebenarnya adalah definisi yang diparafrasa. Itulah yang dipanggil: identiti logaritma asas.

      Sebenarnya, apakah yang berlaku jika nombor b dinaikkan kepada kuasa sedemikian sehingga nombor b kepada kuasa ini memberikan nombor a? Betul: hasilnya adalah nombor yang sama a. Baca perenggan ini dengan teliti sekali lagi - ramai orang terjebak padanya.

      Seperti formula untuk berpindah ke pangkalan baharu, identiti logaritma asas kadangkala merupakan satu-satunya penyelesaian yang mungkin.

      [Kapsyen untuk gambar]

      Perhatikan bahawa log 25 64 = log 5 8 - kita hanya mengambil kuasa dua daripada asas dan hujah logaritma. Dengan mengambil kira peraturan untuk mendarab kuasa dengan asas yang sama, kita mendapat:

      [Kapsyen untuk gambar]

      Jika ada yang tidak tahu, ia adalah cabaran sebenar daripada Peperiksaan Negeri Bersatu :)

      Unit logaritma dan sifar logaritma

      Sebagai kesimpulan, saya akan memberikan dua identiti yang hampir tidak boleh dipanggil sifat - sebaliknya, ia adalah akibat daripada takrifan logaritma. Mereka sentiasa muncul dalam masalah dan, secara mengejutkan, mencipta masalah walaupun untuk pelajar "maju".

      1. log a a = 1 ialah unit logaritma. Ingat sekali dan untuk semua: logaritma kepada mana-mana asas a asas itu sendiri adalah sama dengan satu.
      2. log a 1 = 0 ialah sifar logaritma. Asas a boleh menjadi apa-apa, tetapi jika hujah mengandungi satu, logaritma adalah sama dengan sifar! Kerana 0 = 1 adalah akibat langsung dari definisi.

      Itu semua sifatnya. Pastikan anda berlatih mempraktikkannya! Muat turun helaian panduan pada permulaan pelajaran, cetak dan selesaikan masalah.

      Logaritma. Sifat logaritma (penambahan dan penolakan).

      Sifat logaritma ikut dari definisinya. Dan jadi logaritma nombor itu b berdasarkan A ditakrifkan sebagai eksponen yang mana nombor mesti dinaikkan a untuk mendapatkan nombor b(logaritma hanya wujud untuk nombor positif).

      Daripada rumusan ini berikutan bahawa pengiraan x=log a b, adalah bersamaan dengan menyelesaikan persamaan a x =b. Sebagai contoh, log 2 8 = 3 kerana 8 = 2 3 . Perumusan logaritma memungkinkan untuk mewajarkan bahawa jika b=a c, kemudian logaritma nombor itu b berdasarkan a sama Dengan. Jelas juga bahawa topik logaritma berkait rapat dengan topik kuasa.

      Dengan logaritma, seperti mana-mana nombor, anda boleh lakukan operasi tambah, tolak dan berubah dalam setiap cara yang mungkin. Tetapi disebabkan fakta bahawa logaritma bukan nombor biasa sepenuhnya, peraturan khas mereka sendiri terpakai di sini, yang dipanggil sifat utama.

      Menambah dan menolak logaritma.

      Mari kita ambil dua logaritma dengan asas yang sama: log a x Dan log a y. Kemudian adalah mungkin untuk melakukan operasi tambah dan tolak:

      Seperti yang kita lihat, hasil tambah logaritma sama dengan logaritma hasil darab, dan perbezaan logaritma- logaritma hasil bagi. Lebih-lebih lagi, ini benar jika nombor A, X Dan di positif dan a ≠ 1.

      Adalah penting untuk ambil perhatian bahawa aspek utama dalam formula ini adalah asas yang sama. Jika alasannya berbeza, peraturan ini tidak terpakai!

      Peraturan untuk menambah dan menolak logaritma dengan asas yang sama dibaca bukan sahaja dari kiri ke kanan, tetapi juga sebaliknya. Akibatnya, kita mempunyai teorem untuk logaritma hasil darab dan logaritma hasil bagi.

      Logaritma produk dua nombor positif sama dengan jumlah logaritma mereka ; menghuraikan teorem ini kita mendapat yang berikut jika nombor A, x Dan di positif dan a ≠ 1, Itu:

      Logaritma hasil bagi dua nombor positif adalah sama dengan perbezaan antara logaritma dividen dan pembahagi. Dengan kata lain, jika nombor A, X Dan di positif dan a ≠ 1, Itu:

      Mari kita gunakan teorem di atas untuk menyelesaikannya contoh:

      Jika nombor x Dan di adalah negatif, maka formula logaritma produk menjadi tidak bermakna. Oleh itu, dilarang menulis:

      kerana ungkapan log 2 (-8) dan log 2 (-4) tidak ditakrifkan sama sekali (fungsi logaritma di= log 2 X ditakrifkan hanya untuk nilai hujah positif X).

      Teorem produk terpakai bukan sahaja untuk dua, tetapi juga untuk bilangan faktor yang tidak terhad. Ini bermakna bahawa untuk setiap semula jadi k dan sebarang nombor positif x 1 , x 2 , . . . ,x n terdapat identiti:

      daripada teorem hasil bagi logaritma Satu lagi sifat logaritma boleh diperolehi. Umum mengetahui bahawa log a 1= 0, oleh itu

      Ini bermakna terdapat persamaan:

      Logaritma dua nombor salingan atas sebab yang sama akan berbeza antara satu sama lain semata-mata oleh tanda. Jadi:

      Logaritma. Sifat logaritma

      Logaritma. Sifat logaritma

      Mari kita pertimbangkan kesaksamaan. Beritahu kami nilai dan dan kami ingin mencari nilai .

      Iaitu, kita sedang mencari eksponen yang kita perlukan untuk menaikkannya untuk mendapatkan .

      biarlah pembolehubah boleh mengambil sebarang nilai sebenar, maka sekatan berikut dikenakan ke atas pembolehubah: o" title="a>o"/> , 1″ title="a1″/>, 0″ title="b>0″ />

      Jika kita mengetahui nilai dan , dan kita berhadapan dengan tugas mencari yang tidak diketahui, maka untuk tujuan ini kita memperkenalkan operasi matematik yang dipanggil logaritma.

      Untuk mencari nilai yang kita ambil logaritma sesuatu nombor Oleh asas :

      Logaritma nombor ke pangkalannya ialah eksponen yang mesti dinaikkan untuk mendapatkan .

      iaitu identiti logaritma asas:

      o» title=»a>o»/> , 1″ title=»a1″/>, 0″ title=»b>0″/>

      pada asasnya adalah tatatanda matematik definisi logaritma.

      Operasi matematik logaritma ialah songsang bagi operasi eksponen, jadi sifat logaritma berkait rapat dengan sifat-sifat ijazah.

      Mari kita senaraikan yang utama sifat logaritma:

      (o" title="a>o"/> , 1″ title=»a1″/>, 0″ title=»b>0″/>, 0,

      d>0″/>, 1″ tajuk=”d1″/>

      4.

      5.

      Kumpulan sifat berikut membolehkan anda mewakili eksponen ungkapan di bawah tanda logaritma, atau berdiri di pangkal logaritma dalam bentuk pekali di hadapan tanda logaritma:

      6.

      7.

      8.

      9.

      Kumpulan formula seterusnya membolehkan anda beralih daripada logaritma dengan asas tertentu kepada logaritma dengan asas sewenang-wenangnya, dan dipanggil formula untuk peralihan ke pangkalan baru:

      10.

      12. (akibat daripada harta 11)

      Tiga sifat berikut tidak begitu diketahui, tetapi ia sering digunakan semasa menyelesaikan persamaan logaritma, atau apabila memudahkan ungkapan yang mengandungi logaritma:

      13.

      14.

      15.

      Kes khas:

      — logaritma perpuluhan

      — logaritma semula jadi

      Apabila memudahkan ungkapan yang mengandungi logaritma, pendekatan umum digunakan:

      1. Memperkenalkan perpuluhan dalam bentuk yang biasa.

      2. Kami mewakili nombor bercampur sebagai pecahan tak wajar.

      3. Kami menguraikan nombor di pangkal logaritma dan di bawah tanda logaritma kepada faktor mudah.

      4. Kami cuba mengurangkan semua logaritma kepada asas yang sama.

      5. Gunakan sifat logaritma.

      Mari kita lihat contoh ungkapan memudahkan yang mengandungi logaritma.

      Contoh 1.

      Kira:

      Mari kita permudahkan semua eksponen: tugas kita ialah mengurangkannya kepada logaritma, yang asasnya adalah nombor yang sama dengan asas eksponen.

      ==(oleh harta 7)=(oleh harta 6) =

      Mari kita gantikan penunjuk yang kita dapat ke dalam ungkapan asal. Kami mendapat:

      Jawapan: 5.25

      Contoh 2. Kira:

      Mari kita kurangkan semua logaritma kepada asas 6 (dalam kes ini, logaritma daripada penyebut pecahan akan "berhijrah" kepada pengangka):

      Mari kita uraikan nombor di bawah tanda logaritma kepada faktor mudah:

      Mari gunakan sifat 4 dan 6:

      Mari perkenalkan penggantinya

      Kami mendapat:

      Jawapan: 1

      Logaritma . Identiti logaritma asas.

      Sifat logaritma. Logaritma perpuluhan. Logaritma semula jadi.

      Logaritma nombor positif N kepada asas (b > 0, b 1) ialah eksponen x yang mana b mesti dinaikkan untuk mendapatkan N .

      Entri ini bersamaan dengan yang berikut: b x = N .

      Contoh: log 3 81 = 4, kerana 3 4 = 81;

      log 1/3 27 = – 3, sejak (1/3) - 3 = 3 3 = 27.

      Takrifan logaritma di atas boleh ditulis sebagai identiti:

      Sifat asas logaritma.

      2) log 1 = 0, sejak b 0 = 1 .

      3) Logaritma hasil darab adalah sama dengan jumlah logaritma faktor:

      4) Logaritma hasil bagi adalah sama dengan perbezaan antara logaritma dividen dan pembahagi:

      5) Logaritma kuasa adalah sama dengan hasil darab eksponen dan logaritma asasnya:

      Akibat harta ini adalah seperti berikut: logaritma akar sama dengan logaritma nombor radikal dibahagikan dengan kuasa punca:

      6) Jika asas logaritma ialah darjah, maka nilainya songsangan eksponen boleh dikeluarkan daripada tanda rima log:

      Dua sifat terakhir boleh digabungkan menjadi satu:

      7) Formula modulus peralihan (iaitu peralihan daripada satu asas logaritma ke asas lain):

      Dalam kes khas apabila N=a kami ada:

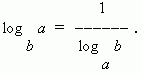
      Logaritma perpuluhan dipanggil logaritma asas 10. Ia ditetapkan lg, i.e. log 10 N= log N. Logaritma nombor 10, 100, 1000, . p ialah 1, 2, 3, …, masing-masing, i.e. mempunyai banyak perkara positif

      unit, berapa banyak sifar yang terdapat dalam nombor logaritma selepas satu. Logaritma nombor 0.1, 0.01, 0.001, . p masing-masing ialah –1, –2, –3, …, i.e. mempunyai sebanyak yang negatif kerana terdapat sifar dalam nombor logaritma sebelum satu (termasuk integer sifar). Logaritma nombor lain mempunyai bahagian pecahan yang dipanggil mantissa. Seluruh bahagian logaritma dipanggil ciri. Untuk kegunaan praktikal, logaritma perpuluhan adalah paling mudah.

      Logaritma semula jadi dipanggil logaritma asas e. Ia dilambangkan dengan ln, i.e. log e N= log N. Nombor e adalah tidak rasional, nilai anggarannya ialah 2.718281828. Ia adalah had ke mana nombor itu cenderung (1 + 1 / n) n dengan peningkatan tanpa had n(cm. pertama had yang indah pada halaman "Had". urutan nombor»).
      Walaupun kelihatan aneh, logaritma semula jadi ternyata sangat mudah apabila menjalankan pelbagai jenis operasi yang berkaitan dengan analisis fungsi. Mengira logaritma kepada asas e dijalankan dengan lebih pantas berbanding sebab lain.